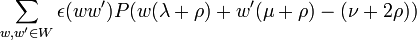Steinberg formula

In mathematical representation theory, Steinberg's formula, introduced by Steinberg (1961), describes the multiplicity of an irreducible representation of a semisimple complex Lie algebra in a tensor product of two irreducible representations. It is a consequence of the Weyl character formula, and for the Lie algebra sl₂ it is essentially the Clebsch–Gordan formula.

Steinberg's formula states that the multiplicity of the irreducible representation of highest weight ν in the tensor product of the irreducible representations with highest weights λ and μ is given by

\sum_{w,w^\prime\in W} \epsilon(ww^\prime)P(w(\lambda+\rho)+w^\prime(\mu+\rho)-(\nu+2\rho))

where W is the Weyl group, ε is the determinant of an element of the Weyl group, ρ is the Weyl vector, and P is the Kostant partition function giving the number of ways of writing a vector as a sum of positive roots.

References

Bourbaki, Nicolas (2005) [1975], Lie groups and Lie algebras. Chapters 7–9, Elements of Mathematics (Berlin), Berlin, New York: Springer-Verlag, ISBN 978-3-540-43405-4, MR 2109105
Steinberg, Robert (1961), "A general Clebsch–Gordan theorem", Bulletin of the American Mathematical Society 67: 406–407, doi:10.1090/S0002-9904-1961-10644-7, ISSN 0002-9904, MR 0126508

This article is issued from Wikipedia - version of the Friday, December 19, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.