Stefan adhesion

Stefan adhesion is the normal stress (force per unit area) acting between two discs when their separation is attempted. Stefan's law governs the flow of a viscous fluid between the solid parallel plates and thus the forces acting when the plates are approximated or separated. 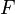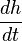The force $F$ resulting at distance $h$ between two parallel circular disks of radius $R$ , immersed in a Newtonian fluid with viscosity $\eta$ , at time $t$ , depends on the rate of change of separation $\frac{d h}{d t}$ :

F=\frac{3\pi \eta\ R^4}{2h^3} \frac{d h}{d t}

Stefan adhesion is mentioned in conjunction with bioadhesion by mucus-secreting animals.^[1] Such systems are much more complex when the fluid is non-Newtonian or inertial effects are relevant (high flow rate).

References

↑ Smith AM (2002). "The Structure and Function of Adhesive Gels from Invertebrates.". Integr. Comp. Biol. 42 (6): 1164–1171. doi:10.1093/icb/42.6.1164.

This article is issued from Wikipedia - version of the Friday, January 15, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.