State-Action-Reward-State-Action

Wikiversity has learning materials about SARSA

State-Action-Reward-State-Action (SARSA) is an algorithm for learning a Markov decision process policy, used in the reinforcement learning area of machine learning. It was introduced in a technical note ^[1] where the alternative name SARSA was only mentioned as a footnote.

This name simply reflects the fact that the main function for updating the Q-value depends on the current state of the agent "S₁", the action the agent chooses "A₁", the reward "R" the agent gets for choosing this action, the state "S₂" that the agent will now be in after taking that action, and finally the next action "A₂" the agent will choose in its new state. Taking every letter in the quintuple (s_t, a_t, r_t, s_t+1, a_t+1) yields the word SARSA.^[2]

Algorithm

A SARSA agent will interact with the environment and update the policy based on actions taken, known as an on-policy learning algorithm. As expressed above, the Q value for a state-action is updated by an error, adjusted by the learning rate alpha. Q values represent the possible reward received in the next time step for taking action a in state s, plus the discounted future reward received from the next state-action observation. Watkin's Q-learning was created as an alternative to the existing temporal difference technique and which updates the policy based on the maximum reward of available actions. The difference may be explained as SARSA learns the Q values associated with taking the policy it follows itself, while Watkin's Q-learning learns the Q values associated with taking the exploitation policy while following an exploration/exploitation policy. For further information on the exploration/exploitation trade off, see reinforcement learning.

Some optimizations of Watkin's Q-learning may also be applied to SARSA, for example in the paper "Fast Online Q(λ)" (Wiering and Schmidhuber, 1998) the small differences needed for SARSA(λ) implementations are described as they arise.

Influence of variables on the algorithm

Learning rate (alpha)

The learning rate determines to what extent the newly acquired information will override the old information. A factor of 0 will make the agent not learn anything, while a factor of 1 would make the agent consider only the most recent information.

Discount factor (gamma)

The discount factor determines the importance of future rewards. A factor of 0 will make the agent "opportunistic" by only considering current rewards, while a factor approaching 1 will make it strive for a long-term high reward. If the discount factor meets or exceeds 1, the 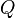values may diverge.

Initial conditions (Q(s₀, a₀))

Since SARSA is an iterative algorithm, it implicitly assumes an initial condition before the first update occurs. A high (infinite) initial value, also known as "optimistic initial conditions",^[3] can encourage exploration: no matter what action will take place, the update rule will cause it to have lower values than the other alternative, thus increasing their choice probability. Recently, it was suggested that the first reward r could be used to reset the initial conditions. According to this idea, the first time an action is taken the reward is used to set the value of Q. This will allow immediate learning in case of fix deterministic rewards. Surprisingly, this resetting-of-initial-conditions (RIC) approach seems to be consistent with human behaviour in repeated binary choice experiments.^[4]

See also

• Reinforcement learning
• Temporal difference learning
• Q-learning

References