Standardized moment

In probability theory and statistics, the kth standardized moment of a probability distribution is 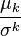$\frac{\mu_k}{\sigma^k}\!$ where $\mu_k$ is the kth moment about the mean and σ is the standard deviation.

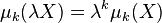It is the normalization of the kth moment with respect to standard deviation. The power of k is because moments scale as $x^k$ , meaning that $\mu_k(\lambda X) = \lambda^k \mu_k(X)$ : they are homogeneous polynomials of degree k, thus the standardized moment is scale invariant. This can also be understood as being because moments have dimension; in the above ratio defining standardized moments, the dimensions cancel, so they are dimensionless numbers.

The first standardized moment is zero, because the first moment about the mean is zero
The second standardized moment is one, because the second moment about the mean is equal to the variance (the square of the standard deviation)
The third standardized moment is the skewness
The fourth standardized moment is the historical kurtosis (used in older works)

Note that for skewness and kurtosis alternative definitions exist, which are based on the third and fourth cumulant respectively.

Other normalizations

For more details on this topic, see Normalization (statistics).

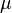Another scale invariant, dimensionless measure for characteristics of a distribution is the coefficient of variation, $\frac{\sigma}{\mu}$ . However, this is not a standardized moment, firstly because it is a reciprocal, and secondly because $\mu$ is the first moment about zero (the mean), not the first moment about the mean (which is zero).

See Normalization (statistics) for further normalizing ratios.

Study design	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling stratified cluster Opinion poll Questionnaire

Controlled experiments	Design control optimal Controlled trial Randomized Random assignment Replication Blocking Factorial experiment

Uncontrolled studies	Observational study Natural experiment Quasi-experiment

Statistical inference

Statistical theory

Frequentist inference

Confidence interval Testing hypotheses Power

Unbiased estimators	Mean unbiased minimum-variance Median unbiased

Biased estimators	Maximum likelihood Method of moments Minimum distance Density estimation

Parametric tests	Likelihood-ratio Wald Score

Specific tests

Z (normal) Student's t-test F Shapiro–Wilk Kolmogorov–Smirnov

Goodness of fit	Chi-squared G Sample source (Anderson–Darling) Sample normality (Shapiro–Wilk) Skewness / kurtosis normality (Jarque-Bera) Model comparison (Likelihood-ratio) Model quality (Akaike criterion)

Signed-rank	1-sample (Wilcoxon) 2-sample (Mann–Whitney U) 1-way anova (Kruskal–Wallis)

Bayesian inference

Correlation	Pearson product–moment Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models Multivariate adaptive regression splines (MARS)

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust Heteroscedasticity Homoscedasticity

Generalized linear model	Exponential families Logistic (Bernoulli) / Binomial / Poisson regressions

Partition of variance	Analysis of variance (ANOVA, anova) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical / Multivariate / Time-series / Survival analysis

Categorical

Multivariate

Time-series

General	Decomposition Trend Stationarity Seasonal adjustment Exponential smoothing Cointegration Structural break Granger causality

Specific tests	Dickey–Fuller Johansen Q-statistic (Ljung–Box) Durbin–Watson Breusch–Godfrey

Time domain	Autocorrelation (ACF) partial (PACF) Cross-correlation (XCF) ARMA model ARIMA model (Box–Jenkins) Autoregressive conditional heteroskedasticity (ARCH) Vector autoregression (VAR)

Frequency domain	Spectral density estimation Fourier analysis Wavelet

Survival

Survival function	Kaplan–Meier estimator (product limit) Proportional hazards models Accelerated failure time (AFT) model First hitting time

Hazard function	Nelson–Aalen estimator

Test	Log-rank test

Applications

Biostatistics	Bioinformatics Clinical trials / studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process / quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Commons
WikiProject

This article is issued from Wikipedia - version of the Sunday, December 14, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Standardized moment

Other normalizations

See also