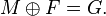Stably free module
In mathematics, a stably free module is a module which is close to being free.
Definition
A finitely generated module M over a ring R is stably free if there exist free finitely generated modules F and G over R such that
Properties
- A projective module is stably free if and only if it possesses a finite free resolution (Theorem XXI.2.1 of Lang's Algebra).
- An infinitely generated module is stably free if and only if it is free.
See also
References
- Page 840 of Lang, Serge (1993), Algebra (Third ed.), Reading, Mass.: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001
This article is issued from Wikipedia - version of the Thursday, April 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.