Square-free word

In combinatorics, a square-free word is a word (a sequence of characters) that does not contain any subword twice in a row.

Thus a square-free word is one that avoids the pattern XX.[1][2]

Examples

Over a two-letter alphabet {a, b} the only square-free words are the empty word and a, b, ab, ba, aba, and bab. However, there exist infinite square-free words in any alphabet with three or more symbols,[3] as proved by Axel Thue.[4][5]

One example of an infinite square-free word over an alphabet of size 3 is the word over the alphabet {0,±1} obtained by taking the first difference of the Thue–Morse sequence.[6][7] That is, from the Thue–Morse sequence

0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, ...

one forms a new sequence in which each term is the difference of two consecutive terms of the Thue–Morse sequence. The resulting square-free word is

1, 0, −1, 1, −1, 0, 1, 0, −1, 0, 1, −1, 1, 0, −1, ... (sequence A029883 in OEIS).

Another example found by John Leech[8] is defined recursively over the alphabet {a, b, c}. Let 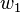w_1 be any word starting with the letter a. Define the words \{w_i \mid i \in \mathbb{N} \} recursively as follows: the word w_{i+1} is obtained from w_i by replacing each a in w_i with abcbacbcabcba, each b with bcacbacabcacb, and each c with cabacbabcabac. It is possible to check that the sequence converges to the infinite square-free word

abcbacbcabcbabcacbacabcacbcabacbabcabacbcacbacabcacb...

Related concepts

A cube-free word is one with no occurrence of www for a factor w. The Thue-Morse sequence is an example of a cube-free word over a binary alphabet.[3] This sequence is not square-free but is "almost" so: the critical exponent is 2.[9] The Thue–Morse sequence has no overlap or overlapping square, instances of 0X0X0 or 1X1X1:[3] it is essentially the only infinite binary word with this property.[10]

The Thue number of a graph G is the smallest number k such that G has a k-coloring for which the sequence of colors along every non-repeating path is squarefree.

The Kolakoski sequence is an example of a cube-free sequence.

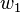An abelian p-th power is a subsequence of the form w_1 \cdots w_p where each w_i is a permutation of w_1. There is no abelian-square-free infinite word over an alphabet of size three: indeed, every word of length eight over such an alphabet contains an abelian square. There is an infinite abelian-square-free word over an alphabet of size five.[11]

Notes

  1. ↑ Lothaire (2011) p.112
  2. ↑ Lothaire (2011) p.114
  3. 1 2 3 Lothaire (2011) p.113
  4. ↑ A. Thue, Über unendliche Zeichenreihen, Norske Vid. Skrifter I Mat.-Nat. Kl., Christiania 7 (1906) 1–22.
  5. ↑ A. Thue, Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen, Norske Vid. Skrifter I Mat.-Nat. Kl., Christiania 1 (1912) 1–67.
  6. ↑ Pytheas Fogg (2002) p.104
  7. ↑ Berstel et al (2009) p.97
  8. ↑ Leech, J. (1957). "A problem on strings of beads". Math. Gazette 41: 277–278. Zbl 0079.01101.
  9. ↑ Krieger, Dalia (2006). "On critical exponents in fixed points of non-erasing morphisms". In Ibarra, Oscar H.; Dang, Zhe. Developments in Language Theory: Proceedings 10th International Conference, DLT 2006, Santa Barbara, CA, USA, June 26-29, 2006. Lecture Notes in Computer Science 4036. Springer-Verlag. pp. 280–291. ISBN 3-540-35428-X. Zbl 1227.68074.
  10. ↑ Berstel et al (2009) p.81
  11. ↑ Blanchet-Sadri, Francine; Simmons, Sean (2011). "Avoiding Abelian Powers in Partial Words". In Mauri, Giancarlo; Leporati, Alberto. Developments in Language Theory. Proceedings, 15th International Conference, DLT 2011, Milan, Italy, July 19-22, 2011. Lecture Notes in Computer Science 6795. Berlin, Heidelberg: Springer-Verlag. pp. 70–81. doi:10.1007/978-3-642-22321-1_7. ISBN 978-3-642-22320-4. ISSN 0302-9743.

References

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.