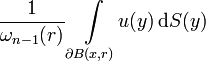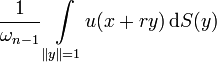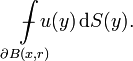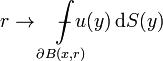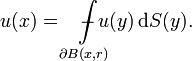Spherical mean
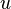 (shown in red) is the average of the values
(shown in red) is the average of the values  (top, in blue) with
(top, in blue) with 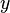 on a "sphere" of given radius around a given point (bottom, in blue).
on a "sphere" of given radius around a given point (bottom, in blue).In mathematics, the spherical mean of a function around a point is the average of all values of that function on a sphere of given radius centered at that point.
Definition
Consider an open set U in the Euclidean space Rn and a continuous function u defined on U with real or complex values. Let x be a point in U and r > 0 be such that the closed ball B(x, r) of center x and radius r is contained in U. The spherical mean over the sphere of radius r centered at x is defined as
where ∂B(x, r) is the (n−1)-sphere forming the boundary of B(x, r), dS denotes integration with respect to spherical measure and ωn−1(r) is the "surface area" of this (n−1)-sphere.
Equivalently, the spherical mean is given by
where ωn−1 is the area of the (n−1)-sphere of radius 1.
The spherical mean is often denoted as
The spherical mean is also defined for Riemannian manifolds in a natural manner.
Properties and uses
- From the continuity of
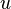 it follows that the function
it follows that the function
- is continuous, and its limit as
 is
is 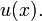
- Spherical means are used in finding the solution of the wave equation
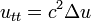 for
for  with prescribed boundary conditions at
with prescribed boundary conditions at 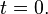
- If
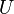 is an open set in
is an open set in  and
and 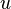 is a C2 function defined on
is a C2 function defined on 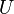 , then
, then 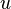 is harmonic if and only if for all
is harmonic if and only if for all  in
in 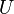 and all
and all  such that the closed ball
such that the closed ball  is contained in
is contained in 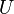 one has
one has
- This result can be used to prove the maximum principle for harmonic functions.
References
- Evans, Lawrence C. (1998). Partial differential equations. American Mathematical Society. ISBN 0-8218-0772-2.
- Sabelfeld, K. K.; Shalimova, I. A. (1997). Spherical means for PDEs. VSP. ISBN 90-6764-211-8.
- Sunada, Toshikazu (1981). "Spherical means and geodesic chains in a Riemannian manifold". Trans. A.M.S. 267: 483–501.