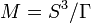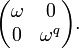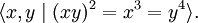Spherical 3-manifold
In mathematics, a spherical 3-manifold M is a 3-manifold of the form
where  is a finite subgroup of SO(4) acting freely by rotations on the 3-sphere
is a finite subgroup of SO(4) acting freely by rotations on the 3-sphere 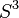 . All such manifolds are prime, orientable, and closed. Spherical 3-manifolds are sometimes called elliptic 3-manifolds or Clifford-Klein manifolds.
. All such manifolds are prime, orientable, and closed. Spherical 3-manifolds are sometimes called elliptic 3-manifolds or Clifford-Klein manifolds.
Properties
A spherical 3-manifold has a finite fundamental group isomorphic to Γ itself. The elliptization conjecture, proved by Grigori Perelman, states that conversely all 3-manifolds with finite fundamental group are spherical manifolds.
The fundamental group is either cyclic, or is a central extension of a dihedral, tetrahedral, octahedral, or icosahedral group by a cyclic group of even order. This divides the set of such manifolds into 5 classes, described in the following sections.
The spherical manifolds are exactly the manifolds with spherical geometry, one of the 8 geometries of Thurston's geometrization conjecture.
Cyclic case (lens spaces)
The manifolds 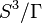 with Γ cyclic are precisely the 3-dimensional lens spaces. A lens space is not determined by its fundamental group (there are non-homeomorphic lens spaces with isomorphic fundamental groups); but any other spherical manifold is.
with Γ cyclic are precisely the 3-dimensional lens spaces. A lens space is not determined by its fundamental group (there are non-homeomorphic lens spaces with isomorphic fundamental groups); but any other spherical manifold is.
Three-dimensional lens spaces arise as quotients of 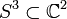 by
the action of the group that is generated by elements of the form
by
the action of the group that is generated by elements of the form
where  . Such a lens space
. Such a lens space 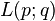 has fundamental group
has fundamental group 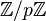 for all
for all 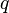 , so spaces with different
, so spaces with different  are not homotopy equivalent.
Moreover, classifications up to homeomorphism and homotopy equivalence are known, as follows. The three-dimensional spaces
are not homotopy equivalent.
Moreover, classifications up to homeomorphism and homotopy equivalence are known, as follows. The three-dimensional spaces 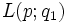 and
and
 are:
are:
- homotopy equivalent if and only if
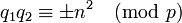 for some
for some 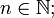
- homeomorphic if and only if
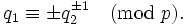
In particular, the lens spaces L(7,1) and L(7,2) give examples of two 3-manifolds that are homotopy equivalent but not homeomorphic.
The lens space L(1,0) is the 3-sphere, and the lens space L(2,1) is 3 dimensional real projective space.
Lens spaces can be represented as Seifert fiber spaces in many ways, usually as fiber spaces over the 2-sphere with at most two exceptional fibers, though the lens space with fundamental group of order 4 also has a representation as a Seifert fiber space over the projective plane with no exceptional fibers.
Dihedral case (prism manifolds)
A prism manifold is a closed 3-dimensional manifold M whose fundamental group is a central extension of a dihedral group.
The fundamental group π1(M) of M is a product of a cyclic group of order m with a group having presentation
for integers k, m, n with k ≥ 1, m ≥ 1, n ≥ 2 and m coprime to 2n.
Alternatively, the fundamental group has presentation
for coprime integers m, n with m ≥ 1, n ≥ 2. (The n here equals the previous n, and the m here is 2k-1 times the previous m.)
We continue with the latter presentation. This group is a metacyclic group of order 4mn with abelianization of order 4m (so m and n are both determined by this group). The element y generates a cyclic normal subgroup of order 2n, and the element x has order 4m. The center is cyclic of order 2m and is generated by x2, and the quotient by the center is the dihedral group of order 2n.
When m = 1 this group is a binary dihedral or dicyclic group. The simplest example is m = 1, n = 2, when π1(M) is the quaternion group of order 8.
Prism manifolds are uniquely determined by their fundamental groups: if a closed 3-manifold has the same fundamental group as a prism manifold M, it is homeomorphic to M.
Prism manifolds can be represented as Seifert fiber spaces in two ways.
Tetrahedral case
The fundamental group is a product of a cyclic group of order m with a group having presentation
for integers k, m with k ≥ 1, m ≥ 1 and m coprime to 6.
Alternatively, the fundamental group has presentation
for an odd integer m ≥ 1. (The m here is 3k-1 times the previous m.)
We continue with the latter presentation. This group has order 24m. The elements x and y generate a normal subgroup isomorphic to the quaternion group of order 8. The center is cyclic of order 2m. It is generated by the elements z3 and x2 = y2, and the quotient by the center is the tetrahedral group, equivalently, the alternating group A4.
When m = 1 this group is the binary tetrahedral group.
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber spaces: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 3.
Octahedral case
The fundamental group is a product of a cyclic group of order m coprime to 6 with the binary octahedral group (of order 48) which has the presentation
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber spaces: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 4.
Icosahedral case
The fundamental group is a product of a cyclic group of order m coprime to 30 with the binary icosahedral group (order 120) which has the presentation
When m is 1, the manifold is the Poincaré homology sphere.
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber spaces: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 5.
References
- Peter Orlik, Seifert manifolds, Lecture Notes in Mathematics, vol. 291, Springer-Verlag (1972). ISBN 0-387-06014-6
- William Jaco, Lectures on 3-manifold topology ISBN 0-8218-1693-4
- William Thurston, Three-dimensional geometry and topology. Vol. 1. Edited by Silvio Levy. Princeton Mathematical Series, 35. Princeton University Press, Princeton, New Jersey, 1997. ISBN 0-691-08304-5