Sphere spectrum

In stable homotopy theory, a branch of mathematics, the sphere spectrum S is the initial object in the categoty of spectra. It is the suspension spectrum of S⁰, i.e., a set of two points. Explicitly, the nth space in the sphere spectrum is the n-dimensional sphere Sⁿ, and the structure maps from the suspension of Sⁿ to Sⁿ⁺¹ are the canonical homeomorphisms. The k-th homotopy group of a sphere spectrum is the k-th stable homotopy group of spheres.

The localization of the sphere spectrum at a prime number p is called the local sphere at p and is denoted by .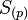

References

• Adams, J. Frank (1974), Stable homotopy and generalised homology, Chicago Lectures in Mathematics, University of Chicago Press, MR 402720