Sphere-world

For the concept in robotics, see Sphere world.

The idea of a sphere-world was constructed by Henri Poincaré who, while pursuing his argument for conventionalism (see philosophy of space and time), offered a thought experiment about a sphere with strange properties.[1]

The concept

Poincaré asks us to imagine a sphere of radius R. The temperature of the sphere decreases from its maximum at the center to absolute zero at its extremity such that a body’s temperature at a distance r from the center is proportional to R^2-r^2.

In addition, all bodies have the same coefficient of dilatation so every body shrinks and expands in similar proportion as they move about the sphere. To finish the story, Poincaré states that the index of refraction will also vary with the distance r, in inverse proportion to R^2-r^2.

How will this world look to inhabitants of this sphere?

In many ways it will look normal. Bodies will remain intact upon transfer from place to place, as well as seeming to remain the same size (the Spherians would shrink along with them). The geometry, on the other hand, would seem quite different. Supposing the inhabitants were to view rods believed to be rigid, or measure distance with light rays. They would find that a geodesic is not a straight line, and that the ratio of a circle’s circumference to its radius is greater than 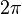2\pi.

These inhabitants would in fact determine that their universe is not ruled by Euclidean geometry, but instead by hyperbolic geometry.

Commentary

This thought experiment is discussed in:

- Roberto Torretti, Philosophy of geometry, from Riemann to Poincaré [2]

- Stanford Encyclopedia of Philosophy, Jeremy Gray, Epistemology of Geometry [3]

This Sphere world is also described in:

- Ian Stewart's Flatterland (chapter 10 , Platterland)

References

  1. ↑ Poincaré, Henri (1952). Science and hypothesis. New York, N.Y.: Dover Publications. p. 51. ISBN 0486602214. Retrieved 17 September 2014 – via Project Gutenberg.
  2. ↑ Torretti, Roberto (1984). Philosophy of geometry from Riemann to Poincaré ([New ed.]. ed.). Dordrecht, Holland: D. Reidel Pub. Co. p. 320. ISBN 9027709203.
  3. ↑ Jeremy Gray. "Epistemology of Geometry". Retrieved 19 September 2014.

See also

This article is issued from Wikipedia - version of the Sunday, January 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.