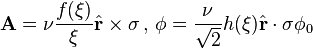Sphaleron

A sphaleron (Greek: σφαλερός "slippery") is a static (time-independent) solution to the electroweak field equations of the Standard Model of particle physics, and it is involved in processes that violate baryon and lepton numbers. Such processes cannot be represented by Feynman diagrams, and are therefore called non-perturbative. Geometrically, a sphaleron is simply a saddle point of the electroweak potential energy (in the infinite-dimensional field space), much like the saddle point of the surface z(x,y)=x2−y2 in three-dimensional analytic geometry.

In the standard model, processes violating baryon number convert three baryons to three antileptons, and related processes. This violates conservation of baryon number and lepton number, but the difference B−L is conserved. In fact, a sphaleron may convert baryons to anti-leptons and anti-baryons to leptons, and hence a quark may be converted to 2 anti-quarks and an anti-lepton, and an anti-quark may be converted to 2 quarks and a lepton. A sphaleron is similar to the midpoint (τ=0) of the instanton, so it is non-perturbative. This means that under normal conditions sphalerons are unobservably rare. However, they would have been more common at the higher temperatures of the early universe.

Sphalerons and baryogenesis

Since a sphaleron may convert baryons to antileptons and antibaryons to leptons, if the density of sphalerons was at some stage high enough, they would wipe out any baryon asymmetry (i.e. any net excess of baryons or anti-baryons). This has two important implications in any theory of baryogenesis within the Standard Model:[1][2]

In some theories of baryogenesis, an imbalance of the number of leptons and antileptons is formed first by leptogenesis and sphaleron transitions then convert this to an imbalance in the numbers of baryons and antibaryons.

Equations

For an SU(2) gauge theory, neglecting 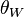\theta_W, we have the following equations for the gauge field and the Higgs field in the gauge A0 = Ar = 0 [3]

\bold{A} = \nu \frac{f(\xi)}{\xi}\hat{\bold{r}}\times\bold{\sigma} \, , \, \phi = \frac{\nu}{\sqrt{2}}h(\xi)\hat{\bold{r}}\cdot\bold{\sigma}\phi_0

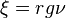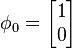where \xi = rg\nu, \phi_0 = \begin{bmatrix}1 \\ 0\end{bmatrix}, the σ-s are the SU(2) generators, g is the electroweak coupling constant ν is the Higgs VEV absolute value.

h(ξ) and f(ξ) are functions going from 0 to 1 as ξ goes from 0 to 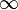\infty. These functions are found numerically.

For a sphaleron in the background of a non-broken phase, the Higgs field must obviously fall off eventually to zero as ξ goes to infinity.

Note that in the limit 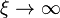\xi\rightarrow\infty, the gauge sector approaches one of the pure-gauge transformation 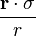\frac{\bold{r}\cdot\bold{\sigma}}{r} , which is the same as the pure gauge transformation to which the BPST instanton approaches as 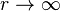r\rightarrow\infty at t=0, hence establishing the connection between the sphaleron and the instanton.

See also

References

  1. ↑ Shaposhnikov, M. E.; Farrar, G. R. (1993). "Baryon Asymmetry of the Universe in the Minimal Standard Model". Physical Review Letters 70: 2833–2836. arXiv:hep-ph/9305274. Bibcode:1993PhRvL..70.2833F. doi:10.1103/PhysRevLett.70.2833.
  2. ↑ Kuzmin, V. A.; Rubakov, V. A.; Shaposhnikov, M. E. (1985). "On anomalous electroweak baryon-number non-conservation in the early universe". Physic Letters B 155: 36–42. Bibcode:1985PhLB..155...36K. doi:10.1016/0370-2693(85)91028-7.
  3. ↑ Arnold, P.; McLerran, L. (1987). "Sphalerons, small fluctuations, and baryon-number violation in electroweak theory". Physical Review D 36: 581–596. Bibcode:1987PhRvD..36..581A. doi:10.1103/PhysRevD.36.581.
This article is issued from Wikipedia - version of the Saturday, February 06, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.