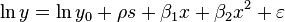Specification (regression)

In regression analysis specification is the process of developing a regression model. This process consists of selecting an appropriate functional form for the model and choosing which variables to include. For instance, one may specify the functional relationship 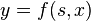between personal income 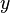and human capital in terms of schooling and on-the-job experience as:^[1]

where is the unexplained error term that is supposed to be independent and identically distributed. If assumptions of the regression model are correct, the least squares estimates of the parameters and 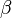will be efficient and unbiased. Hence specification diagnostics usually involve testing the first to fourth moment of the residuals.^[2]

Specification error and bias

Specification error occurs when an independent variable is correlated with the error term. There are several different causes of specification error:

• An incorrect functional form could be employed;
• a variable omitted from the model may have a relationship with both the dependent variable and one or more of the independent variables (omitted-variable bias);^[3]
• an irrelevant variable may be included in the model;
• the dependent variable may be part of a system of simultaneous equations (simultaneity bias);
• measurement errors may affect the independent variables.

Detection

The Ramsey RESET test can help test for specification error.

See also

• Model risk
• Regression model validation

References

• MacKinnon, James G. (1992). "Model Specification Tests and Artificial Regressions". Journal of Economic Literature 30 (1): 102–146. JSTOR 2727880. 
• Thursby, Jerry G.; Schmidt, Peter (September 1977). "Some Properties of Tests for Specification Error in a Linear Regression Model". Journal of the American Statistical Association 72 (359): 635–641. doi:10.1080/01621459.1977.10480627. JSTOR 2286231. 
• Sapra, Sunil (2005). "A regression error specification test (RESET) for generalized linear models" (PDF). Economics Bulletin 3 (1): 1–6. 

Further reading

• Asteriou, Dimitrios; Hall, Stephen G. (2011). "Misspecification: Wrong Regressors, Measurement Errors and Wrong Functional Forms". Applied Econometrics (Second ed.). London: Palgrave MacMillan. pp. 172–197. 
• Gujarati, Damodar N.; Porter, Dawn C. (2009). "Econometric Modeling: Model Specification and Diagnostic Testing". Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 467–522. ISBN 978-0-07-337577-9. 
• Kmenta, Jan (1986). Elements of Econometrics (Second ed.). New York: Macmillan. pp. 442–455. ISBN 0-02-365070-2. 
• Leamer, Edward E. (1978). Specification Searches: Ad hoc Inference with Nonexperimental Data. New York: Wiley. ISBN 0-471-01520-2. 
• Maddala, G. S.; Lahiri, Kajal (2009). "Diagnostic Checking, Model Selection, and Specification Testing". Introduction to Econometrics (Fourth ed.). Chichester: Wiley. pp. 401–449. ISBN 978-0-470-01512-4.