Solid solution strengthening
Solid solution strengthening is a type of alloying that can be used to improve the strength of a pure metal. The technique works by adding atoms of one element (the alloying element) to the crystalline lattice of another element (the base metal). The alloying element diffuses into the matrix, forming a solid solution. In most binary systems, when alloyed above a certain concentration, a second phase will form. The equivalent branch of metallurgy is Intermetallic alloys.
Types
Depending on the size of the alloying element, a substitutional solid solution or an interstitial solid solution can form. In both cases, the overall crystal structure is essentially unchanged.
Substitutional solid solution strengthening occurs when the solute atom is large enough that it can replace solvent atoms in their lattice positions. According to the Hume-Rothery rules, solvent and solute atoms must differ in atomic size by less than 15% in order to form this type of solution. Because both elements exist in the same crystalline lattice, both elements in their pure form must be of the same crystal structure. Examples of substitutional solid solutions include the Cu-Ni and the Ag-Au FCC binary systems, and the Mo-W BCC binary system.
Interstitial solid solutions form when the solute atom is equal to or slightly smaller and can fill the interstices of the solvent atoms. The atoms crowd into the interstitial sites, causing the bonds of the solvent atoms to compress and thus deform. Elements commonly used to form interstitial solid solutions include H, Li, Na, N, C, and O. Carbon in iron (steel) is one example of interstitial solid solution.
Mechanism
The strength of a material is dependent on how easily dislocations in its crystal lattice can be propagated. These dislocations create stress fields within the material depending on their character. When solute atoms are introduced, local stress fields are formed that interact with those of the dislocations, impeding their motion and causing an increase in the yield stress of the material, which means an increase in strength of the material. This gain is a result of both lattice distortion and the modulus effect.
When solute and solvent atoms differ in size, local stress fields are created. Depending on their relative locations, solute atoms will either attract or repel dislocations in their vicinity. This is known as the size effect. This allows the solute atoms to relieve either tensile or compressive strain in the lattice, which in turn puts the dislocation in a lower energy state. In substitutional solid solutions, these stress fields are spherically symmetric, meaning they have no shear stress component. As such, substitutional solute atoms do not interact with the shear stress fields characteristic of screw dislocations. Conversely, in interstitial solid solutions, solute atoms cause a tetragonal distortion, generating a shear field that can interact with both edge, screw, and mixed dislocations. The attraction or repulsion of the dislocation centers to the solute particles increase the stress it takes to propagate the dislocation in any other direction. Increasing the applied stress to move the dislocation increases the yield strength of the material.
The energy density of a dislocation is dependent on its Burgers vector as well as the modulus of the local atoms. When the modulus of solute atoms differs from that of the host element, the local energy around the dislocation is changed, increasing the amount of force necessary to move past this energy well. This is known as the modulus effect. Meanwhile, in the specific case of a lattice distortion, the difference in lattice parameter leads to a high stress field around that solute atom that impedes dislocation movement.
Surface carburizing, or case hardening, is one example of solid solution strengthening in which the density of solute carbon atoms is increased close to the surface of the steel, resulting in a gradient of carbon atoms throughout the material. This provides superior mechanical properties to the surface of the steel.
Governing equations
Solid solution strengthening increases yield strength of the material by increasing the stress 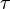 to move dislocations:
to move dislocations:
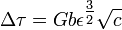
where c is the concentration of the solute atoms, G is the shear modulus, b is the magnitude of the Burger's vector, and  is the lattice strain due to the solute. This is composed of two terms, one describing lattice distortion and the other local modulus change.
is the lattice strain due to the solute. This is composed of two terms, one describing lattice distortion and the other local modulus change.
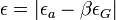 Here,
Here, 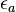 is the lattice distortion term,
is the lattice distortion term, 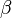 a constant dependent on the solute atoms and
a constant dependent on the solute atoms and 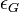 the term that captures the local modulus change.
the term that captures the local modulus change.
The lattice distortion term can be described as:
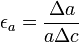 , where a is the lattice parameter of the material.
, where a is the lattice parameter of the material.
Meanwhile, the local modulus change is captured in the following expression:
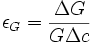 , where G is shear modulus of the solute material,
, where G is shear modulus of the solute material,
Implications
In order to achieve noticeable material strengthening via solute solution strengthening one should alloy with solutes of higher shear modulus, hence increasing the local shear modulus in the material. In addition, one should alloy with elements of different equilibrium lattice constants. The greater the difference in lattice parameter, the higher the local stress fields introduced by alloying. Alloying with elements of higher shear modulus or of very different lattice parameters will increase the stiffness and introduce local stress fields respectively. In either case, the dislocation propagation will be hindered at these sites, impeding plasticity and increasing yield strength proportionally with solute concentration.
Solid solution strengthening depends on:
- Concentration of solute atoms
- Shear modulus of solute atoms
- Size of solute atoms
- Valency of solute atoms (for ionic materials)
Nevertheless, one should not add so much solute as to precipitate a new phase. This occurs if the concentration of the solute reaches a certain critical point given by the binary system phase diagram. This critical concentration therefore puts a limit to the amount of solid solution strengthening that can be achieved with a given material.