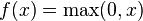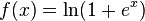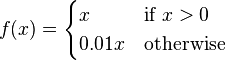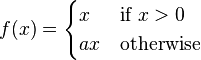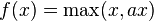Rectifier (neural networks)

In the context of artificial neural networks, the rectifier is an activation function defined as
where x is the input to a neuron. This is also known as a ramp function, and it is analogous to half-wave rectification in electrical engineering. This activation function has been argued to be more biologically plausible[1] than the widely used logistic sigmoid (which is inspired by probability theory; see logistic regression) and its more practical[2] counterpart, the hyperbolic tangent. The rectifier is, as of 2015, the most popular activation function for deep neural networks.[3]
A unit employing the rectifier is also called a rectified linear unit (ReLU).[4]
A smooth approximation to the rectifier is the analytic function
which is called the softplus function.[5]
The derivative of softplus is 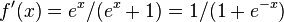 , i.e. the logistic function.
, i.e. the logistic function.
Rectified linear units find applications in computer vision,[1] and speech recognition[6] [7] using deep neural nets.
Variants
Noisy ReLUs
Rectified linear units can be extended to include Gaussian noise, making them noisy ReLUs, giving[4]
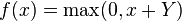 , with
, with 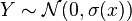
Noisy ReLUs have been used with some success in restricted Boltzmann machines for computer vision tasks.[4]
Leaky ReLUs
Leaky ReLUs allow a small, non-zero gradient when the unit is not active.[7]
Parametric ReLUs take this idea further by making the coefficient of leakage into a parameter that is learned along with the other neural network parameters.[8]
Note that for 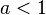 , this is equivalent to
, this is equivalent to
and thus has a relation to "maxout" networks.[8]
Advantages
- Biological plausibility: One-sided, compared to the antisymmetry of tanh.
- Sparse activation: For example, in a randomly initialized network, only about 50% of hidden units are activated (having a non-zero output).
- Efficient gradient propagation: No vanishing gradient problem or exploding effect.
- Efficient computation: Only comparison, addition and multiplication.
For the first time in 2011,[1] the use of the rectifier as a non-linearity has been shown to enable training deep supervised neural networks without requiring unsupervised pre-training. Rectified linear units, compared to sigmoid function or similar activation functions, allow for faster and effective training of deep neural architectures on large and complex datasets.
Potential problems
- Non-differentiable at zero: however it is differentiable at any point arbitrarily close to 0.
See also
References
- 1 2 3 Xavier Glorot, Antoine Bordes and Yoshua Bengio (2011). Deep sparse rectifier neural networks (PDF). AISTATS.
- ↑ Yann LeCun, Leon Bottou, Genevieve B. Orr and Klaus-Robert Müller (1998). "Efficient BackProp" (PDF). In G. Orr and K. Müller. Neural Networks: Tricks of the Trade. Springer.
- ↑ LeCun, Yann; Bengio, Yoshua; Hinton, Geoffrey (2015). "Deep learning". Nature 521: 436–444. doi:10.1038/nature14539.
- 1 2 3 Vinod Nair and Geoffrey Hinton (2010). Rectified linear units improve restricted Boltzmann machines (PDF). ICML.
- ↑ C. Dugas, Y. Bengio, F. Bélisle, C. Nadeau, R. Garcia, NIPS'2000, (2001),Incorporating Second-Order Functional Knowledge for Better Option Pricing
- ↑ László Tóth (2013). Phone Recognition with Deep Sparse Rectifier Neural Networks (PDF). ICASSP.
- 1 2 Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models
- 1 2 Kaiming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun (2015) Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification