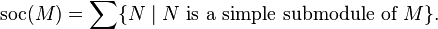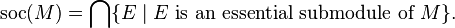Socle (mathematics)

In mathematics, the term socle has several related meanings.

Socle of a group

In the context of group theory, the socle of a group G, denoted soc(G), is the subgroup generated by the minimal normal subgroups of G. It can happen that a group has no minimal non-trivial normal subgroup (that is, every non-trivial normal subgroup properly contains another such subgroup) and in that case the socle is defined to be the subgroup generated by the identity. The socle is a direct product of minimal normal subgroups.^[1]

As an example, consider the cyclic group Z₁₂ with generator u, which has two minimal normal subgroups, one generated by u ⁴ (which gives a normal subgroup with 3 elements) and the other by u ⁶ (which gives a normal subgroup with 2 elements). Thus the socle of Z₁₂ is the group generated by u ⁴ and u ⁶, which is just the group generated by u ².

The socle is a characteristic subgroup, and hence a normal subgroup. It is not necessarily transitively normal, however.

If a group G is a finite solvable group, then the socle can be expressed as a product of elementary abelian p-groups. Thus, in this case, it is just a product of copies of Z/pZ for various p where the same p may occur multiple times in the product.

Socle of a module

In the context of module theory and ring theory the socle of a module M over a ring R is defined to be the sum of the minimal nonzero submodules of M. It can be considered as a dual notion to that of the radical of a module. In set notation,

Equivalently,

The socle of a ring R can refer to one of two sets in the ring. Considering R as a right R module, soc(R_R) is defined, and considering R as a left R module, soc(_RR) is defined. Both of these socles are ring ideals, and it is known they are not necessarily equal.

• If M is an Artinian module, soc(M) is itself an essential submodule of M.
• A module is semisimple if and only if soc(M) = M. Rings for which soc(M) = M for all M are precisely semisimple rings.
• soc(soc(M)) = soc(M).
• M is a finitely cogenerated module if and only if soc(M) is finitely generated and soc(M) is an essential submodule of M.
• Since the sum of semisimple modules is semisimple, the socle of a module could also be defined as the unique maximal semi-simple submodule.
• From the definition of rad(R), it is easy to see that rad(R) annihilates soc(R). If R is a finite-dimensional unital algebra and M a finitely generated R-module then the socle consists precisely of the elements annihilated by the Jacobson radical of R.^[2]

Socle of a Lie algebra

In the context of Lie algebras, a socle of a symmetric Lie algebra is the eigenspace of its structural automorphism which corresponds to the eigenvalue −1. (A symmetric Lie algebra decomposes into the direct sum of its socle and cosocle.)^[3]

See also

• Injective hull
• Radical of a module
• Cosocle

References

• Alperin, J.L.; Bell, Rowen B. (1995). Groups and Representations. Springer-Verlag. p. 136. ISBN 0-387-94526-1. 
• Anderson, Frank Wylie; Fuller, Kent R. (1992). Rings and Categories of Modules. Springer-Verlag. ISBN 978-0-387-97845-1. 

• Robinson, Derek J. S. (1996), A course in the theory of groups, Graduate Texts in Mathematics 80 (2 ed.), New York: Springer-Verlag, pp. xviii+499, ISBN 0-387-94461-3, MR 1357169