Smooth topology

In algebraic geometry, the smooth topology is a certain Grothendieck topology, which is finer than étale topology. Its main use is to define the cohomology of an algebraic stack with coefficients in, say, the étale sheaf .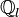

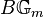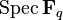To understand the problem that motivates the notion, consider the classifying stack over . Then 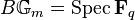in the étale topology;^[1] i.e., just a point. However, we expect the "correct" cohomology ring of 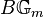to be more like that of 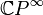as the ring should classify line bundles. Thus, the cohomology of 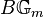should be defined using smooth topology for formulae like Behrend's fixed point formula to hold.

Notes

References

• Behrend, K. Derived l-adic categories for algebraic stacks. Memoirs of the American Mathematical Society Vol. 163, 2003.
• Laumon, Gérard; Moret-Bailly, Laurent (2000), Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics 39, Berlin, New York: Springer-Verlag, ISBN 978-3-540-65761-3, MR 1771927  Unfortunately this book uses the incorrect assertion that morphisms of algebraic stacks induce morphisms of lisse-étale topoi. Some of these errors were fixed by Olsson (2007).