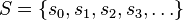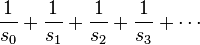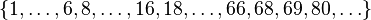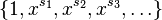Large set (combinatorics)

For other uses of the term, see Small set (disambiguation).

In combinatorial mathematics, a large set of positive integers

S = \{s_0,s_1,s_2,s_3,\dots\}

is one such that the infinite sum of the reciprocals

\frac{1}{s_0}+\frac{1}{s_1}+\frac{1}{s_2}+\frac{1}{s_3}+\cdots

diverges. A small set is any subset of the positive integers that is not large; that is, one whose sum of reciprocals converges.

Large sets appear in the Müntz–Szász theorem and in the Erdős conjecture on arithmetic progressions.

Examples

Every finite subset of the positive integers is small.

The set 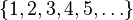$\{1,2,3,4,5,\dots\}$ of all positive integers is known to be a large set; this statement is equivalent to the divergence of the harmonic series. More generally, any arithmetic progression (i.e., a set of all integers of the form an + b with a ≥ 1, b ≥ 1 and n = 0, 1, 2, 3, ...) is a large set.

The set of square numbers is small (see Basel problem). So is the set of cube numbers, the set of 4th powers, and so on. More generally, the set of positive integer values of any polynomial of degree 2 or larger forms a small set.

The set {1, 2, 4, 8, ...} of powers of 2 is known to be a small set, and so is any geometric progression (i.e., a set of numbers of the form of the form abⁿ with a ≥ 1, b ≥ 2 and n = 0, 1, 2, 3, ...).

The set of prime numbers has been proven to be large. The set of twin primes has been proven to be small (see Brun's constant).

The set of prime powers which are not prime (i.e., all numbers of the form pⁿ with n ≥ 2 and p prime) is a small set although the primes are a large set. This property is frequently used in analytic number theory. More generally, the set of perfect powers is small.

The set of numbers whose expansions in a given base exclude a given digit is small. For example, the set

\{1, \dots, 6, 8, \dots, 16, 18, \dots, 66, 68, 69, 80, \dots \}

of integers whose decimal expansion does not include the digit 7 is small. Such series are called Kempner series.

Properties

Every subset of a small set is small.
The union of finitely many small sets is small, because the sum of two convergent series is a convergent series. (In set theoretic terminology, the small sets form an ideal.)
The complement of every small set is large.
The Müntz–Szász theorem states that a set 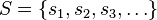$S=\{s_1,s_2,s_3,\dots\}$ is large if and only if the set of polynomials spanned by

\{1,x^{s_1},x^{s_2},x^{s_3},\dots\} \,

is dense in the uniform norm topology of continuous functions on a closed interval. This is a generalization of the Stone–Weierstrass theorem.

Open problems involving large sets

Paul Erdős famously asked the question of whether any set that does not contain arbitrarily long arithmetic progressions must necessarily be small. He offered a prize of $3000 for the solution to this problem, more than for any of his other conjectures, and joked that this prize offer violated the minimum wage law.^[1] This question is still open.

It is not known how to identify whether a given set is large or small in general. As a result, there are many sets which are not known to be either large or small.

Notes

↑ Carl Pomerance, Paul Erdős, Number Theorist Extraordinaire. (Part of the article The Mathematics of Paul Erdős), in Notices of the AMS, January, 1998.

References

A. D. Wadhwa (1975). An interesting subseries of the harmonic series. American Mathematical Monthly 82 (9) 931–933. JSTOR 2318503

This article is issued from Wikipedia - version of the Wednesday, December 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.