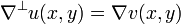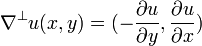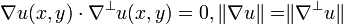Skew gradient

In mathematics, a skew gradient of a harmonic function over a simply connected domain with two real dimensions is a vector field that is everywhere orthogonal to the gradient of the function and that has the same magnitude as the gradient.

Definition

The skew gradient can be defined using complex analysis and the Cauchy–Riemann equations.

Let 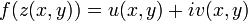$f(z(x,y))=u(x,y)+iv(x,y)$ be a complex-valued analytic function, where u,v are real-valued scalar functions of the real variables x, y.

A skew gradient is defined as:

\nabla^\perp u(x,y)=\nabla v(x,y)

and from the Cauchy–Riemann equations, it is derived that

\nabla^\perp u(x,y)=(-\frac{\partial u}{\partial y},\frac{\partial u}{\partial x})

Properties

The skew gradient has two interesting properties. It is everywhere orthogonal to the gradient of u, and of the same length:

\nabla u(x,y) \cdot \nabla^\perp u(x,y)=0 , \rVert \nabla u\rVert =\rVert \nabla^\perp u\rVert

References

Peter Olver, Introduction to Partial Differential Equations, ch. 7, p. 232

This article is issued from Wikipedia - version of the Wednesday, January 20, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.