Size effect on structural strength

According to the classical theories of elastic or plastic structures made from a material with non-random strength (ft), the nominal strength (σN) of a structure is independent of the structure size (D) when geometrically similar structures are considered.[1] Any deviation from this property is called the size effect. For example, conventional strength of materials predicts that a large beam and a tiny beam will fail at the same stress if they are made of the same material. In the real world, because of size effects, a larger beam will fail at a lower stress than a smaller beam.
The structural size effect concerns structures made of the same material, with the same microstructure. It must be distinguished from the size effect of material inhomogeneities, particularly the Hall-Petch effect, which describes how the material strength increases with decreasing grain size in polycrystalline metals.
The size effect can have two causes:
- statistical, due to material strength randomness, and
- energetic (and non-statistical), due to energy release when a large crack or a large fracture process zone (FPZ) containing damaged material develops before the maximum load is reached.
The limitations of elasticity theory are discussed in good textbooks on the topic. The same holds for plasticity theory. Modern computational models do not have these limitations and they predict structural strength correctly for any size. The scientists that develop new material models make sure that the results agree with the size effect laws. The engineers that design exceptionally large structures make sure that the calculations do not include a size effect mistake.
Statistical Theory of Size Effect in Brittle Structures
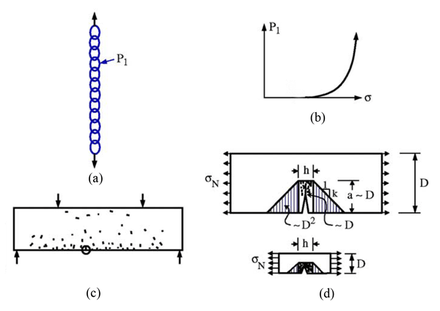
The statistical size effect occurs for a broad class of brittle structures that follow the weakest-link model. This model means that macro-fracture initiation from one material element, or more precisely one representative volume element (RVE), causes the whole structure to fail, like the failure of one link in a chain (Fig. 1a). Since the material strength is random, the strength of the weakest material element in the structure (Fig. 1a) is likely to decrease with increasing structure size  (as noted already by Mariotte in 1684).
(as noted already by Mariotte in 1684).
Denoting the failure probabilities of structure as  and of one RVE under stress
and of one RVE under stress 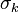 as
as 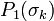 , and noting that the survival probability of a chain is the joint probability of survival of all its
, and noting that the survival probability of a chain is the joint probability of survival of all its  links, one readily concludes that
links, one readily concludes that
-
![1 - P_f = \prod_{k=1}^N [1 - P_1(\sigma_k)]](../I/m/068a4aab645ed3d2ae548f2c0231e9aa.png)
(1)
The key is the left tail of the distribution of 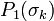 . It was not successfully identified until Weibull in 1939 recognized that the tail is a power law. Denoting the tail exponent as
. It was not successfully identified until Weibull in 1939 recognized that the tail is a power law. Denoting the tail exponent as  , one can then show that, if the structure is sufficiently larger than one RVE (i.e., if N/l0 → ∞), the failure probability of a structure as a function of
, one can then show that, if the structure is sufficiently larger than one RVE (i.e., if N/l0 → ∞), the failure probability of a structure as a function of 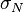 is
is
-
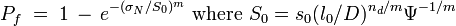
(2)
Eq. 2 is the cumulative Weibull distribution with scale parameter  and shape parameter
and shape parameter  ;
; ![\Psi = \int_V \left[{\hat\sigma}(\xi) \right]^m \, \mbox{d} V(\xi)](../I/m/883319d1c836f90538888f7cf15fbcc7.png) = constant factor depending on the structure geometry,
= constant factor depending on the structure geometry,  = structure volume;
= structure volume;  = relative (size-independent) coordinate vectors,
= relative (size-independent) coordinate vectors, 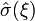 = dimensionless stress field (dependent on geometry), scaled so that the maximum stress be 1;
= dimensionless stress field (dependent on geometry), scaled so that the maximum stress be 1;  = number of spatial dimensions (
= number of spatial dimensions ( = 1, 2 or 3);
= 1, 2 or 3);  = material characteristic length representing the effective size of the RVE (typically about 3 inhomogeneity sizes).
= material characteristic length representing the effective size of the RVE (typically about 3 inhomogeneity sizes).
The RVE is here defined as the smallest material volume whose failure suffices to make the whole
structure fail. From experience, the structure is sufficiently larger than one RVE if the equivalent number 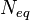 of RVEs in the structure is larger than about
of RVEs in the structure is larger than about  ;
; 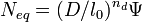 = number of RVEs giving the same
= number of RVEs giving the same  if the stress field is homogeneous (always
if the stress field is homogeneous (always 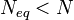 , and usually
, and usually 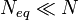 ). For most normal-scale applications to metals and fine-grained ceramics, except for micrometer scale devices, the size is large enough for the Weibull theory to apply (but not for coarse-grained materials such as concrete).
). For most normal-scale applications to metals and fine-grained ceramics, except for micrometer scale devices, the size is large enough for the Weibull theory to apply (but not for coarse-grained materials such as concrete).
From Eq. 2 one can show that the mean strength and the coefficient of variation of strength are obtained as follows:
-
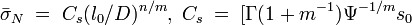
(3)
-
![w \; = \; [\Gamma(1+2m^{-1})\Gamma^{-2}(1+m^{-1})-1]^{1/2}](../I/m/4262dfecbe6db8f876dde729bd534e44.png)
(4)
(where  is the gamma function) The first equation shows that the size effect on the mean nominal strength is
a power function of size
is the gamma function) The first equation shows that the size effect on the mean nominal strength is
a power function of size  , regardless of structure geometry.
, regardless of structure geometry.
Weibull parameter  can be experimentally identified by two methods: 1) The values of
can be experimentally identified by two methods: 1) The values of 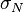 measured on many identical specimens are used to calculate the coefficient of variation of strength, and the value of
measured on many identical specimens are used to calculate the coefficient of variation of strength, and the value of  then follows by solving Eq. (4); or 2) the values of
then follows by solving Eq. (4); or 2) the values of 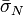 are measured on geometrically similar specimens of several different sizes
are measured on geometrically similar specimens of several different sizes  and the slope of their linear regression in the plot of
and the slope of their linear regression in the plot of 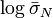 versus
versus 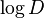 gives
gives 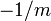 . Method 1 must give the same result for different sizes, and method 2 the same as method 1. If not, the size effect is partly or totally non-Weibullian. Omission of testing for different sizes has often led to incorrect conclusions. Another check is that the histogram of the strengths of many identical specimens must be a straight line when plotted in the Weibull scale. A deviation to the right at high strength range means that
. Method 1 must give the same result for different sizes, and method 2 the same as method 1. If not, the size effect is partly or totally non-Weibullian. Omission of testing for different sizes has often led to incorrect conclusions. Another check is that the histogram of the strengths of many identical specimens must be a straight line when plotted in the Weibull scale. A deviation to the right at high strength range means that 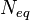 is too small and the material quasibrittle.
is too small and the material quasibrittle.
Energetic Size Effect
The fact that the Weibull size effect is a power law means that it is self-similar, i.e., no characteristic structure size 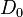 exists, and
exists, and  and material inhomogeneities are negligible compared to
and material inhomogeneities are negligible compared to  . This is the case for fatigue-embrittled metals or fine-grained ceramics except on the micrometer scale. The existence of a finite
. This is the case for fatigue-embrittled metals or fine-grained ceramics except on the micrometer scale. The existence of a finite 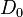 is a salient feature of the energetic size effect, discovered in 1984. This kind of size effect represents a transition between two power laws and is observed in brittle heterogenous materials, termed quasibrittle. These materials include concrete, fiber composites, rocks, coarse-grained and toughened ceramics, rigid foams, sea ice, dental ceramics, dentine, bone, biological shells, many bio- and bio-inspired materials, masonry, mortar, stiff cohesive soils, grouted soils, consolidated snow, wood, paper, carton, coal, cemented sands, etc. On the micro- or nano scale, all the brittle materials become quasibrittle, and thus must exhibit the energetic size effect.
is a salient feature of the energetic size effect, discovered in 1984. This kind of size effect represents a transition between two power laws and is observed in brittle heterogenous materials, termed quasibrittle. These materials include concrete, fiber composites, rocks, coarse-grained and toughened ceramics, rigid foams, sea ice, dental ceramics, dentine, bone, biological shells, many bio- and bio-inspired materials, masonry, mortar, stiff cohesive soils, grouted soils, consolidated snow, wood, paper, carton, coal, cemented sands, etc. On the micro- or nano scale, all the brittle materials become quasibrittle, and thus must exhibit the energetic size effect.
A pronounced energetic size effect occurs in shear, torsional and punching failures of reinforced concrete, in pullout of anchors from concrete, in compression failure of slender reinforced concrete columns and prestressed concrete beams, in compression and tensile failures of fiber-polymer composites and sandwich structures, and in the failures of all the aforementioned quasibrittle materials. One may distinguish two basic types of this size effect.
Type 1: Structures that fail at crack initiation
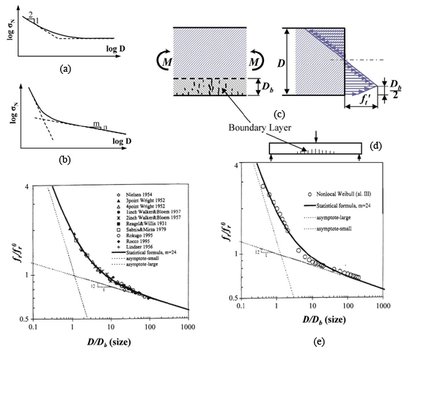
When the macro-crack initiates from one RVE whose size is not negligible compared to the structure size, the deterministic size effect dominates over the statistical size effect. What causes the size effect is a stress redistribution in the structure (Fig. 2c) due to damage in the initiating RVE, which is typically located at fracture surface.
A simple intuitive justification of this size effect may be given by considering the flexural failure of an unnotched simply supported beam under a concentrated load  at midspan (Fig. 2d). Due to material heterogeneity, what decides the maximum load
at midspan (Fig. 2d). Due to material heterogeneity, what decides the maximum load  is not the elastically calculated stress
is not the elastically calculated stress 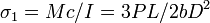 at the tensile face, where
at the tensile face, where 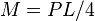 = bending moment,
= bending moment,  = beam depth,
= beam depth, 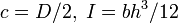 and
and  = beam width. Rather, what decides is the stress value
= beam width. Rather, what decides is the stress value 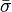 roughly at distance
roughly at distance 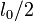 from the tensile face, which is at the middle of FPZ (2c). Noting that
from the tensile face, which is at the middle of FPZ (2c). Noting that 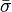 =
= 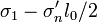 , where
, where 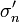 = stress gradient =
= stress gradient = 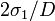 and
and 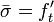 = intrinsic tensile strength of the material, and considering the failure condition
= intrinsic tensile strength of the material, and considering the failure condition 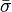 =
= 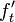 , one gets
, one gets 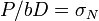 =
= 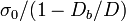 where
where 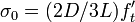 , which is a constant because for geometrically similar beams
, which is a constant because for geometrically similar beams 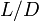 = constant. This expression is valid only for small enough
= constant. This expression is valid only for small enough 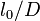 , and so (according to the first two terms of the binomial expansion) one may approximate it as
, and so (according to the first two terms of the binomial expansion) one may approximate it as
-
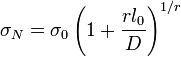
(5)
which is the law of Type 1 deterministic size effect (Fig. 2a). The purpose of the approximation made is: (a) to prevent 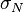 from becoming negative for very small
from becoming negative for very small  , for which the foregoing argument does not apply; and (b) to satisfy the asymptotic condition that the deterministic size effect must vanish for
, for which the foregoing argument does not apply; and (b) to satisfy the asymptotic condition that the deterministic size effect must vanish for 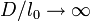 . Here
. Here  = positive empirical constant; the values
= positive empirical constant; the values  = or 2 have been used for concrete, while
= or 2 have been used for concrete, while 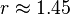 is optimum according to the existing test data from the literature (Fig. 2d).
is optimum according to the existing test data from the literature (Fig. 2d).
A fundamental derivation of Eq. 5 for a general structural geometry has been given by applying dimensional analysis and asymptotic matching to the limit case of energy release when the initial macro-crack length tends to zero. For general structures, the following effective size may be substituted in Eq. (5):
-
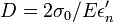
(6)
where 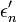 = strain gradient at the maximum strain point located at the surface, in the direction
normal to the surface.
= strain gradient at the maximum strain point located at the surface, in the direction
normal to the surface.
Eq. 5 cannot apply for large sizes because it approaches for 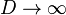 a horizontal asymptote.
For large sizes,
a horizontal asymptote.
For large sizes, 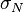 must approach the Weibull statistical size effect, Eq. 3. This condition is satisfied by the generalized energetic-statistical size effect law:
must approach the Weibull statistical size effect, Eq. 3. This condition is satisfied by the generalized energetic-statistical size effect law:
-
![\bar \sigma_N = \sigma_0 \left[ \left( \frac{l_0} D \right)^{r n_d/m}
+\ \frac{r l_0}D\ \right]^{1/r}](../I/m/f5d13a7f8825712c2ba0eac570f0e122.png)
(7)
where 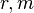 are empirical constants (
are empirical constants (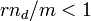 ). The deterministic formula (5) is recovered as the limit case for
). The deterministic formula (5) is recovered as the limit case for 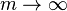 . (Fig. 2d) shows a comparison of the last formula with the test results for many different concretes, plotted as dimensionless strength
. (Fig. 2d) shows a comparison of the last formula with the test results for many different concretes, plotted as dimensionless strength 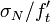 versus dimensionless structure size
versus dimensionless structure size 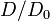 .
.
The probabilistic theory of Type 1 size effect can be derived from fracture nano-mechanics. Kramer’s
transition rate theory shows that, on the nano-scale, the far-left tail of the probability distribution of nano-scale strength  is a power law of the type
is a power law of the type 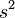 . Analysis of the multiscale transition to the material macro-scale then shows that the RVE strength distribution is Gaussian but with a Weibull (or power-law) left tail whose exponent
. Analysis of the multiscale transition to the material macro-scale then shows that the RVE strength distribution is Gaussian but with a Weibull (or power-law) left tail whose exponent  is much larger than 2 and is grafted roughly at the probability of about 0.001.
is much larger than 2 and is grafted roughly at the probability of about 0.001.
For structures with 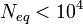 , which are common for quasibrittle materials, the Weibull theory does not apply. But the underlying weakest-link model, expressed by Eq. (1) for
, which are common for quasibrittle materials, the Weibull theory does not apply. But the underlying weakest-link model, expressed by Eq. (1) for  , does, albeit with a finite
, does, albeit with a finite  , which is a crucial point. The finiteness of the weakest-link chain model causes major deviations from the Weibull distribution. As the structure size, measured by
, which is a crucial point. The finiteness of the weakest-link chain model causes major deviations from the Weibull distribution. As the structure size, measured by 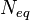 , increases, the grafting point of the Weibullian left part moves to the right until, at about
, increases, the grafting point of the Weibullian left part moves to the right until, at about 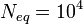 , the entire distribution becomes Weibullian. The mean strength can be computed from this distribution and, as it turns out, its plot is identical with the plot of Eq. 5 seen in Fig. 2g. The point of deviation from the Weibull asymptote is determined by the location of the grafting point on the strength distribution of one RVE (Fig. 2g). Note that the finiteness of the chain in the weakest-link model captures the deterministic part of size effect.
, the entire distribution becomes Weibullian. The mean strength can be computed from this distribution and, as it turns out, its plot is identical with the plot of Eq. 5 seen in Fig. 2g. The point of deviation from the Weibull asymptote is determined by the location of the grafting point on the strength distribution of one RVE (Fig. 2g). Note that the finiteness of the chain in the weakest-link model captures the deterministic part of size effect.
This theory has also been extended to the size effect on the Evans and Paris laws of crack growth in quasibrittle materials, and to the size effect on the static and fatigue lifetimes. It appeared that the size effect on the lifetime is much stronger than it is on the short-time strength (tail exponent  is an order-of-magnitude smaller).
is an order-of-magnitude smaller).
Type 2: Structures in which a large crack or notch exists

The strongest possible size effect occurs for specimens with similar deep notches (Fig. 4b), or for structures in which a large crack, similar for different sizes, forms stably before the maximum load is reached. Because the location of fracture initiation is predetermined to occur at the crack tip and thus cannot sample the random strengths of different RVEs, the statistical contribution to the mean size effect is negligible. Such behavior is typical of reinforced concrete, damaged fiber-reinforced polymers and some compressed unreinforced structures.
The energetic size effect may be intuitively explained by considering the panel in Fig. 1c,d,
initially under a uniform stress equal to  . Introduction of a crack of length
. Introduction of a crack of length  , with a damage zone
of width
, with a damage zone
of width  at the tip, relieves the stress, and thus also the strain energy, from the shaded undamaged triangles of slope
at the tip, relieves the stress, and thus also the strain energy, from the shaded undamaged triangles of slope  on the flanks of the crack. Then, if
on the flanks of the crack. Then, if  and
and 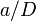 are approximately the same for different sizes, the energy released from the shaded triangles is proportional to
are approximately the same for different sizes, the energy released from the shaded triangles is proportional to 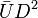 , while the energy dissipated by the fracture process is proportional to
, while the energy dissipated by the fracture process is proportional to 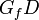 ; here
; here 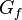 = fracture energy of the material,
= fracture energy of the material, 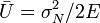 = energy density before fracture, and
= energy density before fracture, and 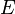 = Young’s elastic modulus. The discrepancy between
= Young’s elastic modulus. The discrepancy between  and
and 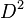 shows that a balance of energy release and dissipation rate can exist for every size
shows that a balance of energy release and dissipation rate can exist for every size  only if
only if 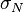 decreases with increasing
decreases with increasing  . If the energy dissipated within the damage zone of width
. If the energy dissipated within the damage zone of width  is added, one obtains the Bažant (1984) size effect law (Type 2):
is added, one obtains the Bažant (1984) size effect law (Type 2):
-
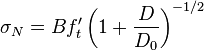
(8)
(Fig. 4c,d) where 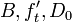 = constants, where
= constants, where 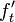 = tensile strength of material, and
= tensile strength of material, and  accounts for the structure geometry.
accounts for the structure geometry.
For more complex geometries such an intuitive derivation is not possible. However, dimensional analysis coupled with asymptotic matching showed that Eq. 8 is applicable in general, and that the dependence of its parameters on the structure geometry has approximately the following form:
-
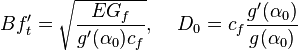
(9)
where 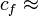 half of the FPZ length,
half of the FPZ length, 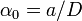 = relative initial crack length (which is constant for geometrically similar scaling);
= relative initial crack length (which is constant for geometrically similar scaling); 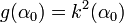 = dimensionless energy release function of linear elastic fracture mechanics (LEFM), which brings about the effect of structure geometry;
= dimensionless energy release function of linear elastic fracture mechanics (LEFM), which brings about the effect of structure geometry; 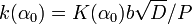 , and
, and  = stress intensity factor. Fitting Eq. 8 to
= stress intensity factor. Fitting Eq. 8 to 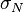 data from tests of geometrically similar notched specimens of very different sizes is a good way to identify the
data from tests of geometrically similar notched specimens of very different sizes is a good way to identify the 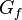 and
and 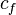 of the material.
of the material.
Size Effect in Cohesive Crack, Crack Band and Nonlocal Models
Numerical simulations of failure by finite element codes can capture the energetic (or deterministic) size effect only if the material law relating the stress to deformation possesses a characteristic length. This was not the case for the classical finite element codes with a material characterized solely by stress-strain relations.
One simple enough computational method is the cohesive (or
fictitious) crack model, in which it is assumed that the stress 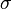 transmitted across a partially opened crack is a decreasing function of the crack opening
transmitted across a partially opened crack is a decreasing function of the crack opening  , i.e.,
, i.e., 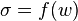 . The area under this function is
. The area under this function is 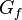 , and
, and
-
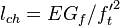
(10)
is the material characteristic length giving rise to the deterministic size effect. An even simpler method is the crack-band model, in which the cohesive crack is replaced in simulations by a crack band of width  equal to one finite element size and a stress-strain relation that is softening in the cross-band direction as
equal to one finite element size and a stress-strain relation that is softening in the cross-band direction as 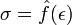 where
where 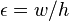 = average strain in that direction.
= average strain in that direction.
When  needs to be adjusted, the softening stress strain relation is adjusted so as to maintain the correct energy dissipation
needs to be adjusted, the softening stress strain relation is adjusted so as to maintain the correct energy dissipation 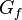 . A more versatile method is the nonlocal damage model in which the stress at a continuum point is a function not of the strain at that point but of the average of the strain field within a certain neighborhood of size
. A more versatile method is the nonlocal damage model in which the stress at a continuum point is a function not of the strain at that point but of the average of the strain field within a certain neighborhood of size  centered at that point. Still another method is the gradient damage model in which the stress depends not only on the strain at that point but also on the gradient of strain. All these computational methods can ensure objectivity and proper convergence with respect to the refinement of the finite element mesh.
centered at that point. Still another method is the gradient damage model in which the stress depends not only on the strain at that point but also on the gradient of strain. All these computational methods can ensure objectivity and proper convergence with respect to the refinement of the finite element mesh.
Fractal Aspects of Size Effect
The fractal properties of material, including the fractal aspect of crack surface roughness and the lacunar fractal aspect of pore structure, may have a role in the size effect in concrete, and may affect the fracture energy of material. However, the fractal properties have yet not been experimentally documented for a broad enough scale and the problem has not yet been studied in depth comparable to the statistical and energetic size effects. The main obstacle to the practical consideration of a fractal influence on the size effect is that, if calibrated for one structure geometry, it is not clear how infer the size effect for another geometry. The pros and cons were discussed, e.g., by Carpinteri et al. (1994, 2001) and Bažant and Yavari (2005).
Practical Importance
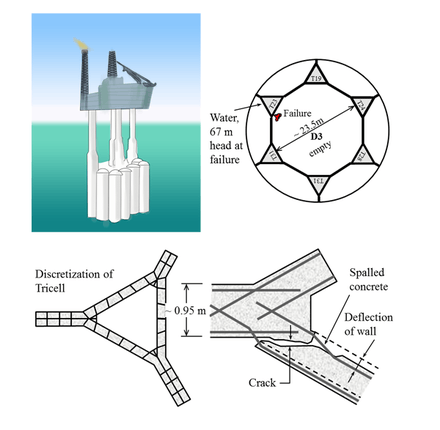
Taking the size effect into account is essential for safe prediction of strength of large concrete bridges, nuclear containments, roof shells, tall buildings, tunnel linings, large load-bearing parts of aircraft, spacecraft and ships made of fiber-polymer composites, wind turbines, large geotechnical excavations, earth and rock slopes, floating sea ice carrying loads, oil platforms under ice forces, etc. Their design depends on the material properties measured on much smaller laboratory specimens. These properties must be extrapolated to sizes greater by one or two orders of magnitude. Even if an expensive full-scale failure test, for example a failure test of the rudder of a very large aircraft, can be carried out, it is financially prohibitive to repeat it thousand times to obtain the statistical distribution of load capacity. Such statistical information, underlying the safety factors, is obtainable only by proper extrapolation of laboratory tests.
The size effect is gaining in importance as larger and larger structures, of more and more slender forms, are being built. The safety factors, of course, give large safety margins—so large that even for the largest civil engineering structures the classical deterministic analysis based on the mean material properties normally yields failure loads smaller than the maximum design loads. For this reasons, the size effect on the strength in brittle failures of concrete structures and structural laminates has long been ignored. Then, however, the failure probability, which is required to be 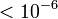 , and actually does have such values for normal-size structures, may become for very large structures as low as
, and actually does have such values for normal-size structures, may become for very large structures as low as 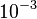 per lifetime. Such high failure probability is intolerable as it adds significantly to the risks to which people are inevitably exposed. In fact, the historical experience shows that very large structures have been failing at a frequency several orders of magnitude higher than smaller ones. The reason it has not led to public outcry is that the large structures are few. But for the locals, who must use the structures daily, the risk is not acceptable.
per lifetime. Such high failure probability is intolerable as it adds significantly to the risks to which people are inevitably exposed. In fact, the historical experience shows that very large structures have been failing at a frequency several orders of magnitude higher than smaller ones. The reason it has not led to public outcry is that the large structures are few. But for the locals, who must use the structures daily, the risk is not acceptable.
Another application is the testing of the fracture energy and characteristic material length. For quasibrittle materials, measuring the size effect on the peak loads (and on the specimen softening after the peak load) is the simplest approach.
Knowing the size effect is also important in the reverse sense—for micrometer scale devices if they are designed partly of fully on the basis of material properties measured more conveniently on the scale of 0.01m to 0.1m.
See also
Notes
- ↑ The nominal strength of a structure (σN) has units of stress and is related to the maximum load (Pmax) that the structure can support. For structures that can be approximated as two-dimensional, σN = Pmax/bD where b is the thickness of the two-dimensional structure. For three-dimensional structures, σN = Pmax/D2. Any structure dimension can be chosen for D but it must be homologous for every size.
References and Bibliography
- Barenblatt, G.I. (1959). “The formation of equilibrium cracks during brittle fracture. General ideas and hypothesis, axially symmetric cracks.” Prikl. Mat. Mekh. 23 (3), 434—444.
- Barenblatt, G.I. (1996). Scaling, Selfsimilarity and Intermediate Asymptotics. Cambridge University Press.
- Barenblatt, G.I. (1978). Similarity, Self-Similarity and Intermediate Asymptotics (in Russian) Girometeoizdat, Moscow; and English translation, Consultants Bureau, New York 1979.
- Barenblatt, G. I. (2003) Scaling, Cambridge University Press.
- Bažant, Z.P. (1976). “Instability, ductility, and size effect in strain-softening concrete.” J. Engng. Mech. Div., Am. Soc. Civil Engrs., 102, EM2, 331—344; disc. 103, 357—358, 775—777, 104, 501—502.
- Bažant, Z.P. (1984). “Size effect in blunt fracture: Concrete, rock, metal.” J. of Engng. Mechanics, ASCE, 110, 518—535.
- Bažant, Z.P. (1997a). “Scaling of quasibrittle fracture: Asymptotic analysis.” Int. J. of Fracture 83 (1), 19—40.
- Bažant, Z.P. (2002). “Scaling of structural strength.” 2nd ed., Elsevier, London 2005.
- Bažant, Z.P., and Chen, E.-P. (1997). “Scaling of structural failure.” Applied Mechanics Reviews ASME 50 (10), 593—627.
- Bažant, Z.P., and Kazemi, M.T. (1990). “Determination of fracture energy, process zone length and brittleness number from size effect, with application to rock and concrete.” Int. J. of Fracture, 44, 111—131.
- Bažant, Z.P., and Novák, D. (2000). “Energetic-statistical size effect in quasibrittle failure at crack initiation.” ACI Materials Journal 97 (3), 381—392.
- Bažant, Z.P., and Planas, J. (1998). Fracture and Size Effect in Concrete and Other Quasibrittle Materials. CRC Press, Boca Raton, Florida.
- Bažant, Z.P., and Yavari, A. (2005). “Is the cause of size effect on structural strength fractal or energetic-statistical?” Engrg. Fracture Mechanics 72, 1--31; with discussion and reply in vol. 74 (2007), p. 2897.
- Bažant, Z. P. (2004) “Scaling theory of quaisbrittle structural failure.” Proc. Nat'l. Acad. Sci., USA 101 (37), 13397-13399.
- Bažant, Z. P., Daniel, I. M., and Li, Z. (1996). “Size effect and fracture characteristics of composite laminates.” J. of Engrg. Materials and Technology ASME 118 (3), 317—324.
- Bažant, Z. P. and Jirásek, M. (2002). “Nonlocal integral formulations of plasticity and damage: Survey of progress.” J. Engrg Mech., ASCE, 128(11), 1119-1149.
- Bažant, Z. P. and Le, J.-L. (2009)“Nano-mechanics based modeling of lifetime distribution of quasibrittle structures”, J. Engrg. Failure Ana., 16, pp 2521–2529
- Bažant, Z. P., Le, J.-L., and Bazant, M. Z. (2009). “Scaling of strength and lifetime distributions of quasibrittle structures based on atomistic fracture mechanics.” Proc. National Acad. of Sciences USA 11484-11489
- Bažant, Z. P., and Pang, S.-D. (2006) “Mechanics based statistics of failure risk of quasibrittle structures and size effect on safety factors.” Proc. Nat'l Acad. Sci., USA 103 (25), pp. 9434–9439.
- Bažant, Z. P., and Pang, S.-D. (2007) “Activation energy based extreme value statistics and size effect in brittle and quasibrittle fracture.” J. Mech. Phys. Solids 55, pp. 91–134.
- Bažant, Z. P., Vořechovský, M., and Novak, D. (2007) “Asymptotic prediction of energetic-statistical size effect from deterministic finite element solutions.” J. Engrg. Mech, ASCE, 128, 153-162.
- Bažant, Z. P. and Xi, Y. (1991) “Statistical size effect in quasi-brittle structures: II. Nonlocal theory.” J. Engrg. Mech., ASCE 117(7), 2623-2640.
- Bažant, Z. P., Zhou, Y., Daniel, I. M., Caner, F. C., and Yu, Q. (2006). “Size effect on strength of laminate-foam sandwich plates”, J. of Engrg. Materials and Technology ASME 128 (3), 366—374.
- Beremin, F.M. (1983). “A local criterion for cleavage fracture of a nuclear pressure vessel steel.” Metallurgy Transactions A, 14, 2277—2287.
- Bouchaud, E. (1997). “Scaling properties of cracks.” J. Phys.: Condens. Matter 9, 4319—4344.
- Carpinteri, A. (1994). “Scaling laws and renormalization groups for strength and toughness of disordered materials.” Int. J. of Solids and Structures 31 (3), 291—302.
- Carpinteri, A., Chiaia, B., and Cornetti, P. (2001). “Static-kinematic duality and the principle of virtual work in the mechanics of fractal media.” Comp. Meth. in Appl. Mech. and Engrg. 19, 3--19.
- Coleman, B. D. (1958) “Statistics and time dependent of mechanical breakdown in fibers.” J. Appl. Phys. 29 (6), pp. 968–983.
- da Vinci, L. (1500's)---see The Notebooks of Leonardo da Vinci (1945), Edward McCurdy, London (p. 546); and Les Manuscrits de Léonard de Vinci, transl. in French by C. Ravaisson-Mollien, Institut de France (1881–91), Vol. 3.
- Fisher, R.A. and Tippett, L.H.C. (1928). “Limiting forms of the frequency distribution of the largest and smallest member of a sample.” Proc., Cambridge Philosophical Society 24, 180—190.
- Fréchet, M. (1927). “Sur la loi de probabilité de l' écart maximum.” Ann. Soc. Polon. Math. 6, p. 93.
- Freudenthal, A.M., and Gumbell, E.J. (1956). “Physical and statistical aspects of fatigue.” in Advances in Applied Mechanics, Vol. 4, Academic Press, 117—157.
- Grassl, P., and Ba žant, Z. P. (2009). “Random lattice-particle simulation of statistical size effect in quasi-brittle structures failing at crack initiation.” J. of Engrg. Mech. ASCE 135 (2), Feb., 85—92.
- Gumbel, E.J. (1958). Statistics of Extremes. Columbia University Press, New York.
- Harlow, D. G. and Phoenix, S. L. (1978) “The Chain-of-Bundles Probability Model For the Strength of Fibrous Materials I: Analysis and Conjectures.” J. Comp. Mater. 12: 195-214
- Harlow, D. G. and Phoenix, S. L. (1979) “Bounds on the probability of failure of composite materials.” Int. J. Frac. 15(4), 312-336
- Hillerborg A. (1985). “The theoretical basis of a method to determine the fracture energy
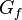 of concrete.” Materials and Structures 18 (106), 291—296.
of concrete.” Materials and Structures 18 (106), 291—296. - Hillerborg, A., Modéer, M. and Petersson, P.E. (1976). “Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements.” Cement and Concrete Research 6 773—782.
- Le, J.-L., and Bažant, Z. P. (2009) “Finite weakest link model with zero threshold for strength distribution of dental restorative ceramics”, Dent. Mater., 25, No. 5, 2009, pp 641–648
- Le, J.-L., and Bažant, Z. P. (2011). “Unified Nano-Mechanics Based Probabilistic Theory of Quasibrittle and Brittle Structures”. J. of the Mech. and Phys. of Solids, in press.
- Mahesh, S. and Phoenix, S. L. (2004) “Lifetime distributions for unidirectional fibrous composites under creep-rupture loading.” Int. J. Fract. 127, pp. 303–360.
- Mariotte, E. (1686). Traité du mouvement des eaux, posthumously edited by M. de la Hire; Engl. transl. by J.T. Desvaguliers, London (1718), p. 249; also Mariotte's collected works, 2nd ed., The Hague (1740).
- Mihashi, H., Okamura, H., and Bažant, Z.P., Editors (1994). Size effect in concrete structures (Proc., Japan Concrete Institute Intern. Workshop held in Sendai, Japan, Oct.31—Nov.2, 1993). E & FN Spon, London-New York, 556 + xiv pages).
- Phoenix, S. L. (1978a) “Stochastic strength and fatigue of fiber bundles.” Int. J. Frac. Vol. 14, No. 3, 327-344.
- Phoenix, S. L. (1978b) “The asymptotic time to failure of a mechanical system of parallel members.” SIAM J. Appl. Maths. Vol. 34, No. 2, 227-246.
- Phoenix, S. L., and Tierney, L.-J. (1983) “A statistical model for the time dependent failure of unidirectional composite materials under local elastic load-sharing among fibers.” Engrg. Fract. Mech. 18 (1), pp. 193–215.
- Phoenix, S. L., Ibnabdeljalil, M., Hui, C.-Y. (1997). “Size effects in the distribution for strength of brittle matrix fibrous composites.” Int. J. Solids Struct. 34(5), 545-568.
- Pijaudier-Cabot, G., and Bažant, Z.P. (1987). “Nonlocal damage theory.” J. of Engrg. Mechanics, ASCE 113 (10), 1512—1533.
- RILEM Committee TC-QFS (2004). “Quasibrittle fracture scaling and size effect---Final report.” Materials and Structures (Paris) 37 (No. 272), 547—586.
- Selected Papers by Alfred M. Freudenthal (1981). Am. Soc. of Civil Engrs., New York.
- Smith, R. L. (1982) “The asymptotic distribution of the strength of a series-parallel system with equal load sharing.” Ann Probab. 10(1), pp. 137 – 171.
- Tierney, L.-J. (1983)“Asymptotic bounds on the time to fatigue failure of bundles of fibers under local load sharing.” Adv. Appl. Prob. Vol 14, No.1, pp 95–121.
- Weibull, W. (1939). “The phenomenon of rupture in solids.” Proc., Royal Swedish Institute of Engineering Research (Ingenioersvetenskaps Akad. Handl.) 153, Stockholm, 1--55.
- Weibull, W. (1949). “A statistical representation of fatigue failures in solids.” Proc., Roy. Inst. of Techn. No. 27.
- Weibull, W. (1951). “A statistical distribution function of wide applicability.” J. of Applied Mechanics ASME, Vol. 18.
- Weibull, W. (1956). “Basic aspects of fatigue.” Proc., Colloquium on Fatigue, Stockholm, Springer—Verlag.
- Xu, X. F. (2007) “A multiscale stochastic finite element method on elliptic problems involving uncertainties.” Comput. Meth. Appl. Mech. Engrg. 196, pp. 2723–2736.
- Zhurkov, S. N. (1965). “Kinetic concept of the strength of solids.” Int. J. Fract. Mech. 1 (4), pp 311–323.
- Stepanov, I. A. (1995). “The scale effect is a consequence of the cellular structure of solid bodies. Thermofluctuation nature of spread in the values of strength.” Materials Science 31 (4), pp 441–447.