Six factor formula

The six-factor formula is used in nuclear engineering to determine the multiplication of a nuclear chain reaction in a non-infinite medium. The formula is^[1]

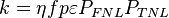
k = \eta f p \varepsilon P_{FNL} P_{TNL}

Symbol	Name	Meaning	Formula	Typical Thermal Reactor Value
$\eta$	Thermal Fission Factor (Eta)	The number of fission neutrons produced per absorption in the fuel.	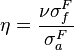$\eta = \frac{\nu \sigma_f^F}{\sigma_a^F}$	1.65
$f$	The thermal utilization factor	Probability that a neutron that gets absorbed does so in the fuel material.	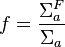$f = \frac{\Sigma_a^F}{\Sigma_a}$	0.71
$p$	The resonance escape probability	Fraction of fission neutrons that manage to slow down from fission to thermal energies without being absorbed.	$p \approx \mathrm{exp} \left( -\frac{\sum\limits_{i=1}^{N} N_i I_{r,A,i}}{\left( \overline{\xi} \Sigma_p \right)_{mod}} \right)$	0.87
$\varepsilon$	The fast fission factor (Epsilon)	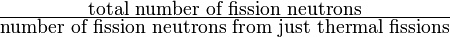$\tfrac{\mbox{total number of fission neutrons}}{\mbox{number of fission neutrons from just thermal fissions}}$	$\varepsilon \approx 1 + \frac{1-p}{p}\frac{u_f \nu_f P_{FAF}}{f \nu_t P_{TAF} P_{TNL}}$	1.02
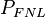$P_{FNL}$	The fast non-leakage probability	The probability that a fast neutron will not leak out of the system.	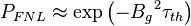$P_{FNL} \approx \mathrm{exp} \left( -{B_g}^2 \tau_{th} \right)$	0.97
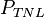$P_{TNL}$	The thermal non-leakage probability	The probability that a thermal neutron will not leak out of the system.	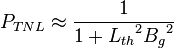$P_{TNL} \approx \frac{1}{1+{L_{th}}^2 {B_g}^2}$	0.99

The symbols are defined as:^[2]

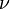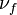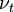$\nu$ , $\nu_f$ and $\nu_t$ are the average number of neutrons produced per fission in the medium (2.43 for Uranium-235).
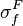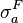$\sigma_f^F$ and $\sigma_a^F$ are the microscopic fission and absorption cross sections for fuel, respectively.
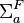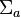$\Sigma_a^F$ and $\Sigma_a$ are the macroscopic absorption cross sections in fuel and in total, respectively.
$N_i$ is the number density of atoms of a specific nuclide.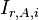
is the resonance integral for absorption of a specific nuclide.
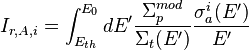- $I_{r,A,i} = \int_{E_{th}}^{E_0} dE' \frac{\Sigma_p^{mod}}{\Sigma_t(E')} \frac{\sigma_a^i(E')}{E'}$ .
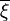is the average lethargy gain per scattering event.
- Lethargy is defined as decrease in neutron energy.
$u_f$ (fast utilization) is the probability that a fast neutron is absorbed in fuel.
$P_{FAF}$ is the probability that a fast neutron absorption in fuel causes fission.
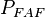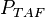$P_{TAF}$ is the probability that a thermal neutron absorption in fuel causes fission.
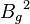${B_g}^2$ is the geometric buckling.
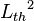is the diffusion length of thermal neutrons.
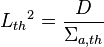- ${L_{th}}^2 = \frac{D}{\Sigma_{a,th}}$ .
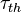is the age to thermal.
- $\tau = \int_{E_{th}}^{E'} dE'' \frac{1}{E''} \frac{D(E'')}{\overline{\xi} \left[ D(E'') {B_g}^2 + \Sigma_t(E') \right]}$ .
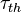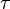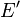- $\tau_{th}$ is the evaluation of $\tau$ where $E'$ is the energy of the neutron at birth.

Multiplication

The multiplication factor, k, is defined as (see Nuclear chain reaction):

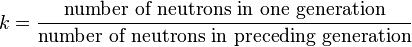
k = \frac{\mbox{number of neutrons in one generation}}{\mbox{number of neutrons in preceding generation}}

If k is greater than 1, the chain reaction is supercritical, and the neutron population will grow exponentially.
If k is less than 1, the chain reaction is subcritical, and the neutron population will exponentially decay.
If k = 1, the chain reaction is critical and the neutron population will remain constant.

References

↑ Duderstadt, James; Hamilton, Louis (1976). Nuclear Reactor Analysis. John Wiley & Sons, Inc. ISBN 0-471-22363-8.
↑ Adams, Marvin L. (2009). Introduction to Nuclear Reactor Theory. Texas A&M University.

This article is issued from Wikipedia - version of the Saturday, November 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Six factor formula

Multiplication

See also

References