Trigonometric integral

In mathematics, the trigonometric integrals are a family of integrals involving trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.
Sine integral
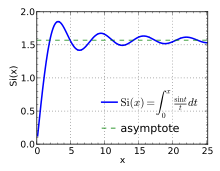
The different sine integral definitions are
By definition, Si(x) is the antiderivative of sin x / x which is zero for x = 0; and si(x) is the antiderivative of sin x / x which is zero for x = ∞. Their difference is given by the Dirichlet integral,
Note that sin x / x is the sinc function, and also the zeroth spherical Bessel function.
In signal processing, the oscillations of the sine integral cause overshoot and ringing artifacts when using the sinc filter, and frequency domain ringing if using a truncated sinc filter as a low-pass filter.
Related is the Gibbs phenomenon: if the sine integral is considered as the convolution of the sinc function with the heaviside step function, this corresponds to truncating the Fourier series, which is the cause of the Gibbs phenomenon.
Cosine integral

The different cosine integral definitions are
where γ is the Euler–Mascheroni constant. Some texts use ci instead of Ci.
Ci(x) is the antiderivative of cos x / x (which vanishes at 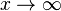 ). The two definitions are related by
). The two definitions are related by
Hyperbolic sine integral
The hyperbolic sine integral is defined as
Hyperbolic cosine integral
The hyperbolic cosine integral is
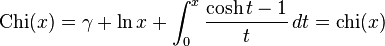 ,
,
where  is the Euler–Mascheroni constant.
is the Euler–Mascheroni constant.
It has the series expansion 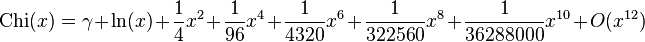 .
.
Auxiliary functions
Trigonometric integrals can be understood in terms of the so-called "auxiliary functions"
![f(x)
\equiv \int_0^\infty \frac{\sin(t)}{t+x} dt = \int_0^\infty \frac{e^{-x t}}{t^2 + 1} dt
= \operatorname{Ci}(x) \sin(x) + \left[\frac{\pi}{2} - \operatorname{Si}(x) \right] \cos(x)](../I/m/0dd8afcaaea943315d2a548cc297416d.png)
![g(x)
\equiv \int_0^\infty \frac{\cos(t)}{t+x} dt = \int_0^\infty \frac{t e^{-x t}}{t^2 + 1} dt
= -\operatorname{Ci}(x) \cos(x) + \left[\frac{\pi}{2} - \operatorname{Si}(x) \right] \sin(x)](../I/m/cf6d518d02a0113d21609f3161d39a28.png) .
.
Using these functions, the trigonometric integrals may be re-expressed as (cf Abramowitz & Stegun, p. 232)
Nielsen's spiral

The spiral formed by parametric plot of si , ci is known as Nielsen's spiral. It is also referred to as the Euler spiral, the Cornu spiral, a clothoid, or as a linear-curvature polynomial spiral.
The spiral is also closely related to the Fresnel integrals. This spiral has applications in vision processing, road and track construction and other areas.
Expansion
Various expansions can be used for evaluation of Trigonometric integrals, depending on the range of the argument.
Asymptotic series (for large argument)
These series are asymptotic and divergent, although can be used for estimates and even precise evaluation at ℜ(x) ≫ 1.
Convergent series
These series are convergent at any complex x, although for |x | ≫ 1 the series will converge slowly initially, requiring many terms for high precision
Relation with the exponential integral of imaginary argument
The function
is called the exponential integral. It is closely related to Si and Ci,
As each respective function is analytic except for the cut at negative values of the argument, the area of validity of the relation should be extended to (Outside this range, additional terms which are integer factors of π appear in the expression.)
Cases of imaginary argument of the generalized integro-exponential function are
which is the real part of
Similarly
Efficient evaluation
Padé approximants of the convergent Taylor series provide an efficient way to evaluate the functions for small arguments.
See also
Signal processing
References
- Abramowitz, Milton; Stegun, Irene A., eds. (December 1972) [1964]. "Chapter 5". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series 55 (10 ed.). New York, USA: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 231. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.8.2. Cosine and Sine Integrals", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Temme, N. M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- Mathar, R. J. (2009). "Numerical evaluation of the oscillatory integral over exp(iπx)·x1/x between 1 and ∞". arXiv:0912.3844., Appendix B.
- Sine Integral Taylor series proof from Dan Sloughter's Difference Equations to Differential Equations.
External links
- http://mathworld.wolfram.com/SineIntegral.html
- Hazewinkel, Michiel, ed. (2001), "Integral sine", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Hazewinkel, Michiel, ed. (2001), "Integral cosine", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
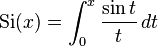
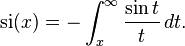
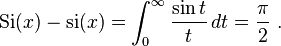
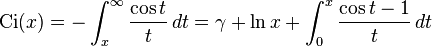
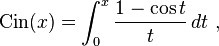
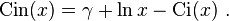
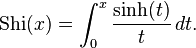
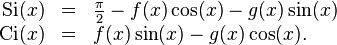
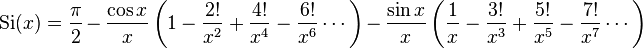
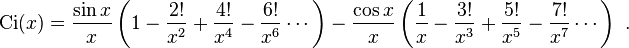
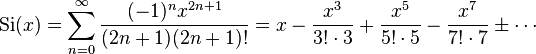
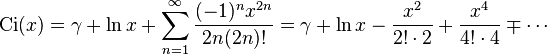
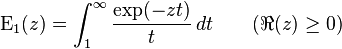
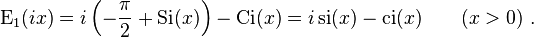
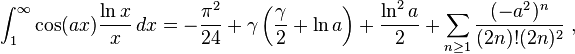
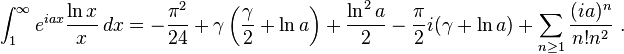
![\int_1^\infty e^{iax}\frac{\ln x}{x^2}dx
=1+ia[-\frac{\pi^2}{24}+\gamma\left(\frac{\gamma}{2}+\ln a-1\right)+\frac{\ln^2 a}{2}-\ln a+1
-\frac{i\pi}{2}(\gamma+\ln a-1)]+\sum_{n\ge 1}\frac{(ia)^{n+1}}{(n+1)!n^2}~.](../I/m/b1e4795abe9bb712ea01fcb9b0ce930b.png)