Simson line

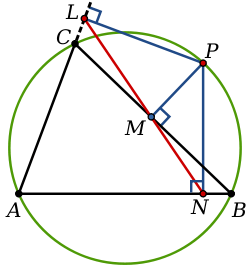
The Simson line LN (red) of the triangle ABC.

In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear.^[1] The line through these points is the Simson line of P, named for Robert Simson.^[2] The concept was first published, however, by William Wallace in 1797.^[3]

The converse is also true; if the three closest points to P on three lines are collinear, and no two of the lines are parallel, then P lies on the circumcircle of the triangle formed by the three lines. Or in other words, the Simson line of a triangle ABC and a point P is just the pedal triangle of ABC and P that has degenerated into a straight line and this condition constrains the locus of P to trace the circumcircle of triangle ABC.

Properties

Simson lines (in red) are tangents to the Steiner deltoid (in blue).

The Simson line of a vertex of the triangle is the altitude of the triangle dropped from that vertex, and the Simson line of the point diametrically opposite to the vertex is the side of the triangle opposite to that vertex.

If P and Q are points on the circumcircle, then the angle between the Simson lines of P and Q is half the angle of the arc PQ. In particular, if the points are diametrically opposite, their Simson lines are perpendicular and in this case the intersection of the lines lies on the nine-point circle.

Let H denote the orthocenter of the triangle ABC, then the Simson line of P bisects the segment PH in a point that lies on the nine-point circle.

Given two triangles with the same circumcircle, the angle between the Simson lines of a point P on the circumcircle for both triangles doesn't depend of P.

The set of all Simson lines, when drawn, form an envelope in the shape of a deltoid known as the Steiner deltoid of the reference triangle.

The construction of the Simson line that coincides with a side of the reference triangle (see first property above) yields a nontrivial point on this side line. This point is the reflection of the foot of the altitude (dropped onto the side line) about the midpoint of the side line being constructed. Furthermore this point is a tangent point between the side of the reference triangle and its Steiner deltoid.

A quadrilateral that is not a parallelogram has one and only one pedal point, called the Simson point, with respect to which the feet on the quadrilateral are collinear.^[4] The Simson point of a trapezoid is the point of intersection of the two nonparallel sides.^[5]^{:p. 186}

No convex polygon with at least 5 sides has a Simson line.^[6]

Proof of existence

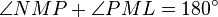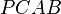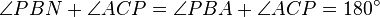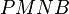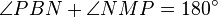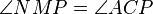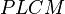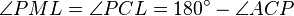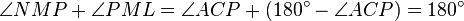The method of proof is to show that $\angle NMP + \angle PML = 180^\circ$ . $PCAB$ is a cyclic quadrilateral, so $\angle PBN + \angle ACP = \angle PBA + \angle ACP = 180^\circ$ . $PMNB$ is a cyclic quadrilateral (Thales' theorem), so $\angle PBN + \angle NMP = 180^\circ$ . Hence $\angle NMP = \angle ACP$ . Now $PLCM$ is cyclic, so $\angle PML = \angle PCL = 180^\circ - \angle ACP$ . Therefore $\angle NMP + \angle PML = \angle ACP + (180^\circ - \angle ACP) = 180^\circ$ .

Generalizations

Generalization 1

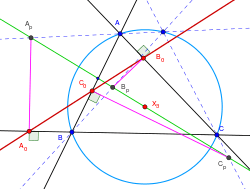
The projections of Ap,Bp,Cp onto BC,CA,AB are three collinear points

Let ABC be a triangle, let a line ℓ through circumcenter O, let a point P lie on circumcircle. Let AP,BP,CP meet ℓ at Ap,Bp,Cp respectively. Let A0,B0,C0 the projections of Ap,Bp,Cp onto BC,CA,AB, respectively. Then A0,B0,C0 are collinear. Moreover, the new line passes through the midpoint of OH, where H the orthocenter of ΔABC. If ℓ passes through P, the line coincides with the Simson line. ^[7]^[8]

A propjective of Simson line

Generalization 2

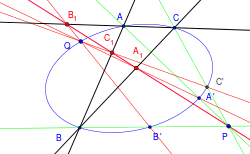
Let a circumconic of the triangle ABC, let Q, P be two points on the plane. Let PA,PB,PC intersect the conic at A1,B1,C1 respectively. QA1 intersects BC at A2, QB1 intersects AC at B2, QC1 intersects AB at C2. Then four points A2,B2,C2,D are colinear if only if Q lie on the conic. ^[9] ^[10] ^[11]

References

↑ H.S.M. Coxeter and S.L. Greitzer, Geometry revisited, Math. Assoc. America, 1967: p.41.
↑ "Gibson History 7 - Robert Simson". 2008-01-30.
↑ "Simson Line from Interactive Mathematics Miscellany and Puzzles". 2008-09-23.
↑ Daniela Ferrarello, Maria Flavia Mammana, and Mario Pennisi, "Pedal Polygons", Forum Geometricorum 13 (2013) 153–164: Theorem 4.
↑ Olga Radko and Emmanuel Tsukerman, "The Perpendicular Bisector Construction, the Isoptic point, and the Simson Line of a Quadrilateral", Forum Geometricorum 12 (2012).
↑ Emmanuel Tsukerman, "On Polygons Admitting a Simson Line as Discrete Analogs of Parabolas", Forum Geometricorum 13 (2013), 197–208.
↑ "A Generalization of Simson Line". 2015-04-19.
↑ Yahoo group, AdvancedPlaneGeometry, conversations, messages 2644
↑ Geoff Smith (2015). 99.20 A projective Simson line. The Mathematical Gazette, 99, pp 339-341. doi:10.1017/mag.2015.47
↑ A Generalization Simson's line, carnot theorem, Collings-Carnort theorem
↑ The point of concurrency lies on the circumcircle

External links

Wikimedia Commons has media related to Simson line.

Simson Line
F. M. Jackson and Weisstein, Eric W., "Simson Line", MathWorld.
A generalization of Neuberg's theorem and the Simson-Wallace line at Dynamic Geometry Sketches, an interactive dynamic geometry sketch.

This article is issued from Wikipedia - version of the Sunday, July 26, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.