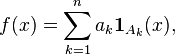Simple function

In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line, similar to a step function. Simple functions are sufficiently 'nice' that using them makes mathematical reasoning, theory, and proof easier. For example simple functions attain only a finite number of values. Some authors also require simple functions to be measurable; as used in practice, they invariably are.

A basic example of a simple function is the floor function over the half-open interval [1,9), whose only values are {1,2,3,4,5,6,7,8}. A more advanced example is the Dirichlet function over the real line, which takes the value 1 if x is rational and 0 otherwise. (Thus the "simple" of "simple function" has a technical meaning somewhat at odds with common language.) Note also that all step functions are simple.

Simple functions are used as a first stage in the development of theories of integration, such as the Lebesgue integral, because it is easy to define integration for a simple function, and also, it is straightforward to approximate more general functions by sequences of simple functions.

Definition

Formally, a simple function is a finite linear combination of indicator functions of measurable sets. More precisely, let (X, Σ) be a measurable space. Let A₁, ..., A_n ∈ Σ be a sequence of disjoint measurable sets, and let a₁, ..., a_n be a sequence of real or complex numbers. A simple function is a function $f: X \to \mathbb{C}$ of the form

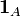f(x)=\sum_{k=1}^n a_k {\mathbf 1}_{A_k}(x),

where ${\mathbf 1}_A$ is the indicator function of the set A.

Properties of simple functions

The sum, difference, and product of two simple functions are again simple functions, and multiplication by constant keeps a simple function simple; hence it follows that the collection of all simple functions on a given measurable space forms a commutative algebra over 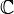$\mathbb{C}$ .

Integration of simple functions

If a measure μ is defined on the space (X,Σ), the integral of f with respect to μ is

\sum_{k=1}^na_k\mu(A_k),

if all summands are finite.

Relation to Lebesgue integration

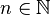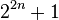Any non-negative measurable function $f\colon X \to\mathbb{R}^{+}$ is the pointwise limit of a monotonic increasing sequence of non-negative simple functions. Indeed, let $f$ be a non-negative measurable function defined over the measure space $(X, \Sigma,\mu)$ as before. For each $n\in\mathbb N$ , subdivide the range of $f$ into $2^{2n}+1$ intervals, 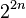$2^{2n}$ of which have length $2^{-n}$ . For each $n$ , set

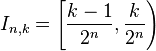I_{n,k}=\left[\frac{k-1}{2^n},\frac{k}{2^n}\right)

for

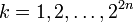k=1,2,\ldots,2^{2n}

, and

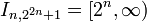I_{n,2^{2n}+1}=[2^n,\infty)

(Note that, for fixed $n$ , the sets $I_{n,k}$ are disjoint and cover the non-negative real line.)

Now define the measurable sets

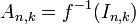A_{n,k}=f^{-1}(I_{n,k}) \,

for

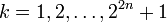k=1,2,\ldots,2^{2n}+1

Then the increasing sequence of simple functions

f_n=\sum_{k=1}^{2^{2n}+1}\frac{k-1}{2^n}{\mathbf 1}_{A_{n,k}}

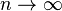converges pointwise to $f$ as $n\to\infty$ . Note that, when $f$ is bounded, the convergence is uniform. This approximation of $f$ by simple functions (which are easily integrable) allows us to define an integral $f$ itself; see the article on Lebesgue integration for more details.

References

J. F. C. Kingman, S. J. Taylor. Introduction to Measure and Probability, 1966, Cambridge.
S. Lang. Real and Functional Analysis, 1993, Springer-Verlag.
W. Rudin. Real and Complex Analysis, 1987, McGraw-Hill.
H. L. Royden. Real Analysis, 1968, Collier Macmillan.

This article is issued from Wikipedia - version of the Thursday, August 06, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.