Sigma-ring

In mathematics, a nonempty collection of sets is called a σ-ring (pronounced sigma-ring) if it is closed under countable union and relative complementation.

Formal definition

Let $\mathcal{R}$ be a nonempty collection of sets. Then $\mathcal{R}$ is a σ-ring if:

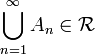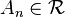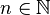
$\bigcup_{n=1}^{\infty} A_{n} \in \mathcal{R}$ if $A_{n} \in \mathcal{R}$ for all $n \in \mathbb{N}$
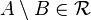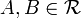
$A \setminus B \in \mathcal{R}$ if $A, B \in \mathcal{R}$

Properties

From these two properties we immediately see that

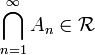\bigcap_{n=1}^{\infty} A_n \in \mathcal{R}

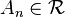A_{n} \in \mathcal{R}

for all

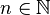
n \in \mathbb{N}

This is simply because 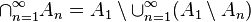$\cap_{n=1}^\infty A_n = A_1 \setminus \cup_{n=1}^{\infty}(A_1 \setminus A_n)$ .

Similar concepts

If the first property is weakened to closure under finite union (i.e., 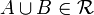$A \cup B \in \mathcal{R}$ whenever 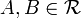$A, B \in \mathcal{R}$ ) but not countable union, then $\mathcal{R}$ is a ring but not a σ-ring.

Uses

σ-rings can be used instead of σ-fields (σ-algebras) in the development of measure and integration theory, if one does not wish to require that the universal set be measurable. Every σ-field is also a σ-ring, but a σ-ring need not be a σ-field.

A σ-ring $\mathcal{R}$ that is a collection of subsets of $X$ induces a σ-field for $X$ . Define $\mathcal{A}$ to be the collection of all subsets of $X$ that are elements of $\mathcal{R}$ or whose complements are elements of $\mathcal{R}$ . Then $\mathcal{A}$ is a σ-field over the set $X$ . In fact $\mathcal{A}$ is the minimal σ-field containing $\mathcal{R}$ since it must be contained in every σ-field containing $\mathcal{R}$ .

References

Walter Rudin, 1976. Principles of Mathematical Analysis, 3rd. ed. McGraw-Hill. Final chapter uses σ-rings in development of Lebesgue theory.

This article is issued from Wikipedia - version of the Thursday, June 18, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.