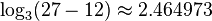Sierpinski sponge

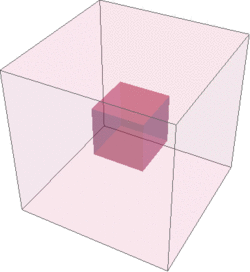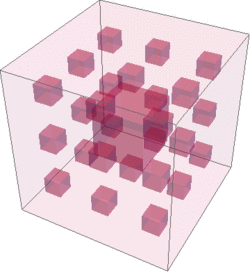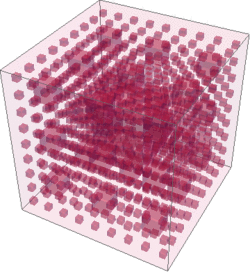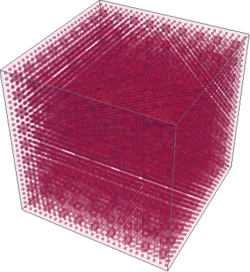
"Jello" plot of the Sierpinski sponge animation through recursion steps. To enable better visibility the darker areas are the holes in the brighter cube. Selected sections cutting the largest cubic cavity parallel to the cube walls show up as the full Sierpinski carpets

Sierpinski sponge (or cube and not the Menger sponge) is the exact three dimensional extension of the Sierpinski carpet. Menger sponge is not the precise three dimensional equivalent of the Sierpinski carpet. Using exactly the logic of the two dimensional construction of the Sierpinski carpet in three space dimensions one should in the next recursion remove only the central scaled cube from the bigger cubes but not also the side cubes. Otherwise in the Sierpinski carpet one should remove five squares forming together the greek cross but not only the one. Obviously the internal fractal structure of such sponge cube is seen only when it is being cut. Because the number of the filling elements is growing now by the 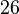$26$ while preserving the carpet scaling factor $1/3$ it is near-three dimensional with the Hausdorff dimension:

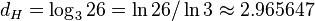
$d_{H}=\log _{3}26=\ln 26/\ln 3\approx 2.965647$

which is more than for the Menger sponge.

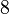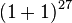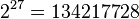In a similar way one may construct other fractal cubes by removing at the each step arbitrary number $N$ of smaller cubes scaled $1/3$ from bigger cubes e.g. the central cube and $8$ corner cubes and in general asymmetrically. Using the $(1+1)^{27}$ binomial expansion as the sum of the all numbers of combinations one may notice that there is $2^{27}=134217728$ asymptotic objects while treating each of the smaller scaled removed or left cubes as different. Most of the cubes constructed in such a way are also strange geometrically in three dimensional space having the Hausdorff dimension:

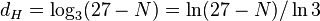
$d_{H}=\log _{3}(27-N)=\ln(27-N)/\ln 3$

which is not the integer. Only recursively removing 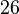$26$ cubes and leaving one at the corner converges to one trivial point with the $0$ dimension.

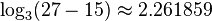
Tree-looking variation of Sierpinski sponge obtained by recursively removing the 8 corner, 6 face-centered and the central cubes (totally 15 cubes) with the fractal dimension $\log _{3}(27-15)\approx 2.261859$
Another tree but Pine-like looking variation obtained by recursively removing 12 edge cubes with the fractal dimension $\log _{3}(27-12)\approx 2.464973$

This article is issued from Wikipedia - version of the Monday, December 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.