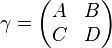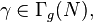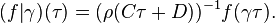Siegel modular form

In mathematics, Siegel modular forms are a major type of automorphic form. These stand in relation to the conventional elliptic modular forms as abelian varieties do in relation to elliptic curves; the complex manifolds constructed as in the theory are basic models for what a moduli space for abelian varieties (with some extra level structure) should be, as quotients of the Siegel upper half-space rather than the upper half-plane by discrete groups.

The modular forms of the theory are holomorphic functions on the set of symmetric n × n matrices with positive definite imaginary part; the forms must satisfy an automorphy condition. Siegel modular forms can be thought of as multivariable modular forms, i.e. as special functions of several complex variables.

Siegel modular forms were first investigated by Carl Ludwig Siegel in the 1930s for the purpose of studying quadratic forms analytically. These primarily arise in various branches of number theory, such as arithmetic geometry and elliptic cohomology. Siegel modular forms have also been used in some areas of physics, such as conformal field theory.

Definition

Preliminaries

Let $g, N \in \mathbb{N}$ and define

\mathcal{H}_g=\left\{\tau \in M_{g \times g}(\mathbb{C}) \ \big| \ \tau^{\mathrm{T}}=\tau, \textrm{Im}(\tau) \text{ positive definite} \right\},

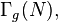the Siegel upper half-space. Define the symplectic group of level $N$ , denoted by $\Gamma_g(N),$ as

\Gamma_g(N)=\left\{ \gamma \in GL_{2g}(\mathbb{Z}) \ \big| \ \gamma^{\mathrm{T}} \begin{pmatrix} 0 & I_g \\ -I_g & 0 \end{pmatrix} \gamma= \begin{pmatrix} 0 & I_g \\ -I_g & 0 \end{pmatrix} , \ \gamma \equiv I_{2g}\mod N\right\},

where $I_g$ is the $g \times g$ identity matrix. Finally, let

\rho:\textrm{GL}_g(\mathbb{C}) \rightarrow \textrm{GL}(V)

be a rational representation, where $V$ is a finite-dimensional complex vector space.

Siegel modular form

Given

\gamma=\begin{pmatrix} A & B \\ C & D \end{pmatrix}

and

\gamma \in \Gamma_g(N),

define the notation

(f\big|\gamma)(\tau)=(\rho(C\tau+D))^{-1}f(\gamma\tau).

Then a holomorphic function

f:\mathcal{H}_g \rightarrow V

is a Siegel modular form of degree $g$ (sometimes called the genus), weight $\rho$ , and level $N$ if

(f\big|\gamma)=f.

In the case that 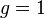$g=1$ , we further require that $f$ be holomorphic 'at infinity'. This assumption is not necessary for $g>1$ due to the Koecher principle, explained below. Denote the space of weight $\rho$ , degree $g$ , and level $N$ Siegel modular forms by

M_{\rho}(\Gamma_g(N)).

Examples

Some methods for constructing Siegel modular forms include:

Eisenstein series
Theta functions of lattices (possibly with a pluri-harmonic polynomial)
Saito–Kurokawa lift for degree 2
Ikeda lift
Miyawaki lift
Products of Siegel modular forms.

Level 1, small degree

For degree 1, the level 1 Siegel modular forms are the same as level 1 modular forms. The ring of such forms is a polynomial ring C[E₄,E₆] in the (degree 1) Eisenstein series E₄ and E₆.

For degree 2, (Igusa 1962, 1967) showed that the ring of level 1 Siegel modular forms is generated by the (degree 2) Eisenstein series E₄ and E₆ and 3 more forms of weights 10, 12, and 35. the ideal of relations between them is generated by the square of the weight 35 form minus a certain polynomial in the others.

For degree 3, Tsuyumine (1986) described the ring of level 1 Siegel modular forms, giving a set of 34 generators.

For degree 4, the level 1 Siegel modular forms of small weights have been found. There are no cusp forms of weights 2, 4, or 6. The space of cusp forms of weight 8 is 1-dimensional, spanned by the Schottky form. The space of cusp forms of weight 10 has dimension 1, the space of cusp forms of weight 12 has dimension 2, the space of cusp forms of weight 14 has dimension 3, and the space of cusp forms of weight 16 has dimension 7 (Poor & Yuen 2007).

For degree 5, the space of cusp forms has dimension 0 for weight 10, dimension 2 for weight 12. The space of forms of weight 12 has dimension 5.

For degree 6, there are no cusp forms of weights 0, 2, 4, 6, 8. The space of Siegel modular forms of weight 2 has dimension 0, and those of weights 4 or 6 both have dimension 1.

Level 1, small weight

For small weights and level 1, Duke & Imamoḡlu (1998) give the following results (for any positive degree):

Weight 0: The space of forms is 1-dimensional, spanned by 1.
Weight 1: The only Siegel modular form is 0.
Weight 2: The only Siegel modular form is 0.
Weight 3: The only Siegel modular form is 0.
Weight 4: For any degree, the space of forms of weight 4 is 1-dimensional, spanned by the theta function of the E₈ lattice (of appropriate degree). The only cusp form is 0.
Weight 5: The only Siegel modular form is 0.
Weight 6: The space of forms of weight 6 has dimension 1 if the degree is at most 8, and dimension 0 if the degree is at least 9. The only cusp form is 0.
Weight 7: The space of cusp forms vanishes if the degree is 4 or 7.
Weight 8:In genus 4, the space of cusp forms is 1-dimensional, spanned by the Schottky form and the space of forms is 2-dimensional. There are no cusp forms if the genus is 8.
There are no cusp forms if the genus is greater than twice the weight.

Table of dimensions of spaces of Siegel cusp forms

Poor & Yuen (2006) and Chenevier & Lannes (2014) gave many of the following results.

Dimensions of spaces of level 1 Siegel cusp forms: Siegel modular forms
Weight	degree 0	degree 1	degree 2	degree 3	degree 4	degree 5	degree 6	degree 7	degree 8	degree 9	degree 10	degree 11	degree 12
0	1: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1
2	1: 1	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0	0: 0
4	1: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1
6	1: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 1	0: 0	0: 0	0: 0	0: 0
8	1: 1	0: 1	0 : 1	0 :1	1: 2	0: 2	0: 2	0: 2	0: 2
10	1: 1	0: 1	1: 2	0 : 2	1:	0:	1:	0:	1:	0:	0:
12	1: 1	1: 2	1: 3	1: 4	2: 6	2: 8	3: 11	3: 14	4: 18	2:20	2: 22	1: 23	1: 24
14	1: 1	0: 1	: 2		3:
16	1: 1	1: 2	: 4		7:
18	1: 1	1: 2	: 4
20	1: 1	1: 2	: 5
22	1: 1	1: 2	: 6
24	1: 1	2: 3	: 8
26	1: 1	1: 2	: 7
28	1: 1	2: 3	: 10
30	1: 1	2: 3	: 11

Koecher principle

The theorem known as the Koecher principle states that if $f$ is a Siegel modular form of weight $\rho$ , level 1, and degree $g>1$ , then $f$ is bounded on subsets of $\mathcal{H}_g$ of the form

\left\{\tau \in \mathcal{H}_g \ | \textrm{Im}(\tau) > \epsilon I_g \right\},

where $\epsilon>0$ . Corollary to this theorem is the fact that Siegel modular forms of degree $g>1$ have Fourier expansions and are thus holomorphic at infinity.^[1]

References

↑ This was proved by Max Koecher, Zur Theorie der Modulformen n-ten Grades I, Mathematische. Zeitschrift 59 (1954), 455–466. A corresponding principle for Hilbert modular forms was apparently known earlier, after Fritz Gotzky, Uber eine zahlentheoretische Anwendung von Modulfunktionen zweier Veranderlicher, Math. Ann. 100 (1928), pp. 411-37

Chenevier, Gaëtan; Lannes, Jean (2014), Formes automorphes et voisins de Kneser des réseaux de Niemeier, arXiv:1409.7616
Duke, W.; Imamoḡlu, Ö. (1998), "Siegel modular forms of small weight", Math. Ann. 310 (1): 73–82, doi:10.1007/s002080050137, MR 1600030
Freitag, E. (1983), Siegelsche Modulfunktionen, Grundlehren der Mathematischen Wissenschaften, 254. Springer-Verlag, Berlin, ISBN 3-540-11661-3, MR 0871067
van der Geer, Gerard (2008), "Siegel modular forms and their applications", The 1-2-3 of modular forms, 181–245, Universitext, Berlin: Springer, arXiv:math/0605346, MR 2409679
Igusa, Jun-ichi (1962), "On Siegel modular forms of genus two", Amer. J. Math. 84: 175–200, doi:10.2307/2372812, MR 0141643
Klingen, Helmut (2003), Introductory Lectures on Siegel Modular Forms, Cambridge University Press, ISBN 0-521-35052-2
Tsuyumine, Shigeaki (1986), "On Siegel modular forms of degree three", Amer. J. Math. 108 (4): 755–862, doi:10.2307/2374517, JSTOR 2374517, MR 0853217

This article is issued from Wikipedia - version of the Sunday, January 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.