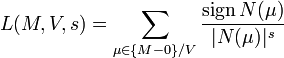Shimizu L-function

In mathematics, the Shimizu L-function, introduced by Shimizu (1963), is a Dirichlet series associated to a totally real algebraic number field. Michael Francis Atiyah, H. Donnelly, and I. M. Singer (1983) defined the signature defect of the boundary of a manifold as the eta invariant, the value as s=0 of their eta function, and used this to show that Hirzebruch's signature defect of a cusp of a Hilbert modular surface can be expressed in terms of the value at s=0 or 1 of a Shimizu L-function.

Definition

Suppose that K is a totally real algebraic number field, M is a lattice in the field, and V is a subgroup of maximal rank of the group of totally positive units preserving the lattice. The Shimizu L-series is given by

References

• Atiyah, Michael Francis; Donnelly, H.; Singer, I. M. (1982), "Geometry and analysis of Shimizu L-functions", Proceedings of the National Academy of Sciences of the United States of America 79 (18): 5751, doi:10.1073/pnas.79.18.5751, ISSN 0027-8424, MR 674920 
• Atiyah, Michael Francis; Donnelly, H.; Singer, I. M. (1983), "Eta invariants, signature defects of cusps, and values of L-functions", Annals of Mathematics. Second Series 118 (1): 131–177, doi:10.2307/2006957, ISSN 0003-486X, MR 707164 
• Shimizu, Hideo (1963), "On discontinuous groups operating on the product of the upper half planes", Annals of Mathematics. Second Series 77: 33–71, doi:10.2307/1970201, ISSN 0003-486X, MR 0145106