Shekel function

Shekel function is a multidimensional, multimodal, continuous, deterministic function commonly used as a test function for testing optimization techniques.

The mathematical form of a function in n dimensions with m maxima is:

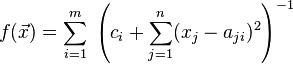
f(\vec{x}) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ji})^2 \right)^{-1}

or, similarly,

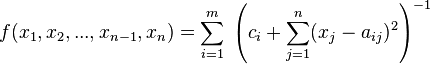
f(x_1,x_2,...,x_{n-1},x_n) = \sum_{i = 1}^{m} \; \left( c_{i} + \sum\limits_{j = 1}^{n} (x_{j} - a_{ij})^2 \right)^{-1}

A Shekel function in 2 dimensions and with 10 maxima

References

Shekel, J. 1971. "Test Functions for Multimodal Search Techniques." Fifth Annual Princeton Conference on Information Science and Systems.

See also

This article is issued from Wikipedia - version of the Friday, October 03, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.