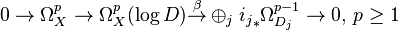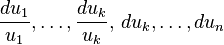Sheaf of logarithmic differential forms

In algebraic geometry, the sheaf of logarithmic differential p-forms 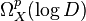$\Omega^p_X(\log D)$ on a smooth projective variety X along a smooth divisor 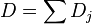$D = \sum D_j$ is defined and fits into the exact sequence of locally free sheaves:

0 \to \Omega^p_X \to \Omega^p_X(\log D) \overset{\beta}\to \oplus_j {i_j}_*\Omega^{p-1}_{D_j} \to 0, \, p \ge 1

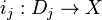where $i_j: D_j \to X$ are the inclusions of irreducible divisors (and the pushforwards along them are extension by zero), and β is called the residue map when p is 1.

For example,^[1] if x is a closed point on 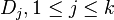$D_j, 1 \le j \le k$ and not on 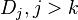$D_j, j > k$ , then

{du_1 \over u_1}, \dots, {du_k \over u_k}, \, du_k, \dots, du_n

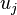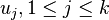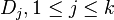form a basis of $\Omega^1_X(\log D)$ at x, where $u_j$ are local coordinates around x such that $u_j, 1 \le j \le k$ are local parameters for $D_j, 1 \le j \le k$ .

References

↑ Deligne, Part II, Lemma 3.2.1.

de Jong, Algebraic de Rham cohomology.
P. Deligne, Equations Différentielles à Points Singuliers Réguliers. Lecture Notes in Math. 163.

This article is issued from Wikipedia - version of the Saturday, June 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Sheaf of logarithmic differential forms

See also

References