Boole's expansion theorem
Boole's expansion theorem, often referred to as the Shannon expansion or decomposition, is the identity:  , where
, where  is any Boolean function and
is any Boolean function and  and
and 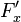 are
are  with the argument
with the argument  equal to
equal to 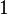 and to
and to  respectively.
respectively.
The terms  and
and 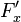 are sometimes called the positive and negative Shannon cofactors, respectively, of
are sometimes called the positive and negative Shannon cofactors, respectively, of  with respect to
with respect to  . These are functions, computed by restrict operator,
. These are functions, computed by restrict operator,  and
and 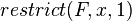 (see valuation (logic) and partial application).
(see valuation (logic) and partial application).
It has been called the "fundamental theorem of Boolean algebra".[1] Besides its theoretical importance, it paved the way for binary decision diagrams, satisfiability solvers, and many other techniques relevant to computer engineering and formal verification of digital circuits.
Statement of the theorem
A more explicit way of stating the theorem is-
Proof for the statement follows from direct use of mathematical induction, from the observation that 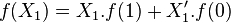 and expanding a 2-ary and n-ary Boolean functions identically.
and expanding a 2-ary and n-ary Boolean functions identically.
History
George Boole presented this expansion as his Proposition II, "To expand or develop a function involving any number of logical symbols", in his Laws of Thought (1854),[2] and it was "widely applied by Boole and other nineteenth-century logicians".[3]
Claude Shannon, noted information-theorist and communications pioneer, mentioned this expansion, among other Boolean identities, in a 1948 paper,[4] and showed the switching network interpretations of the identity. In the literature of computer design and switching theory, it is often attributed to Shannon.[3]
Application to switching circuits
- Binary decision diagrams follow from systematic use of this theorem
- Any Boolean function can be implemented directly in a switching circuit using a hierarchy of basic multiplexer by repeated application of this theorem.
Notes
- ↑ Paul C. Rosenbloom, The Elements of Mathematical Logic, 1950, p. 5
- ↑ George Boole, An Investigation of the Laws of Thought: On which are Founded the Mathematical Theories of Logic and Probabilities, 1854, p. 72 full text at Google Books
- 1 2 Frank Markham Brown, Boolean Reasoning: The Logic of Boolean Equations, 2nd edition, 2003, p. 42
- ↑ Claude Shannon, "The Synthesis of Two-Terminal Switching Circuits", Bell System Technical Journal 28:59–98, full text, p. 62
External links
- Shannon’s Decomposition Example with multiplexers.
- Optimizing Sequential Cycles Through Shannon Decomposition and Retiming (PDF) Paper on application.
