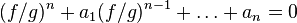Serre's criterion for normality
In algebra, Serre's criterion for normality, introduced by Jean-Pierre Serre, gives necessary and sufficient conditions for a commutative Noetherian ring A to be a normal ring. The criterion involves the following two conditions for A:
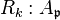 is a regular local ring for any prime ideal
is a regular local ring for any prime ideal  of height ≤ k.
of height ≤ k.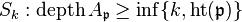 for any prime ideal
for any prime ideal  .[1]
.[1]
The statement is:
- A is a reduced ring
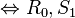 hold.
hold. - A is a normal ring
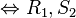 hold.
hold. - A is a Cohen–Macaulay ring
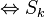 hold for all k.
hold for all k.
Items 1, 3 trivially follow from the definitions. Item 2 is much deeper.
For an integral domain, the criterion is due to Krull. The general case is due to Serre.
Proof
Sufficiency
(After EGA IV. Theorem 5.8.6.)
Suppose A satisfies S2 and R1. Then A in particular satisfies S1 and R0; hence, it is reduced. If 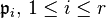 are the minimal prime ideals of A, then the total ring of fractions K of A is the direct product of the residue fields
are the minimal prime ideals of A, then the total ring of fractions K of A is the direct product of the residue fields 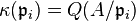 : see total ring of fractions of a reduced ring. That means we can write
: see total ring of fractions of a reduced ring. That means we can write 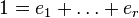 where
where  are idempotents in
are idempotents in 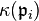 and such that
and such that 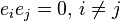 . Now, if A is integrally closed in K, then each
. Now, if A is integrally closed in K, then each  is integral over A and so is in A; consequently, A is a direct product of integrally closed domains Aei's and we are done. Thus, it is enough to show that A is integrally closed in K.
is integral over A and so is in A; consequently, A is a direct product of integrally closed domains Aei's and we are done. Thus, it is enough to show that A is integrally closed in K.
For this end, suppose
where all f, g, ai's are in A and g is moreover a non-zerodivisor. We want to show:
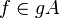 .
.
Now, the condition S2 says that 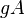 is unmixed of height one; i.e., each associated primes
is unmixed of height one; i.e., each associated primes  of
of 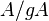 has height one. By the condition R1, the localization
has height one. By the condition R1, the localization 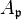 is integrally closed and so
is integrally closed and so 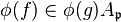 , where
, where 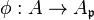 is the localization map, since the integral equation persists after localization. If
is the localization map, since the integral equation persists after localization. If 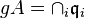 is the primary decomposition, then, for any i, the radical of
is the primary decomposition, then, for any i, the radical of  is an associated prime
is an associated prime  of
of 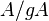 and so
and so 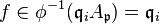 ; the equality here is because
; the equality here is because  is a
is a  -primary ideal. Hence, the assertion holds.
-primary ideal. Hence, the assertion holds.
Necessity
Suppose A is a normal ring. For S2, let  be an associated prime of
be an associated prime of 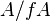 for a non-zerodivisor f; we need to show it has height one. Replacing A by a localization, we can assume A is a local ring with maximal ideal
for a non-zerodivisor f; we need to show it has height one. Replacing A by a localization, we can assume A is a local ring with maximal ideal  . By definition, there is an element g in A such that
. By definition, there is an element g in A such that 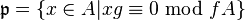 and
and 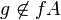 . Put y = g/f in the total ring of fractions. If
. Put y = g/f in the total ring of fractions. If 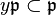 , then
, then  is a faithful
is a faithful ![A[y]](../I/m/a20a573cdd040373678ed348abb338a9.png) -module and is a finitely generated A-module; consequently,
-module and is a finitely generated A-module; consequently, 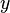 is integral over A and thus in A, a contradiction. Hence,
is integral over A and thus in A, a contradiction. Hence, 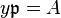 or
or 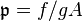 , which implies
, which implies  has height one (Krull's principal ideal theorem).
has height one (Krull's principal ideal theorem).
For R1, we argue in the same way: let  be a prime ideal of height one. Localizing at
be a prime ideal of height one. Localizing at  we assume
we assume  is a maximal ideal and the similar argument as above shows that
is a maximal ideal and the similar argument as above shows that  is in fact principal. Thus, A is a regular local ring.
is in fact principal. Thus, A is a regular local ring. 
Notes
References
- Grothendieck, Alexandre; Dieudonné, Jean (1965). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie". Publications Mathématiques de l'IHÉS 24. doi:10.1007/bf02684322. MR 0199181.
- H. Matsumura, Commutative algebra, 1970.