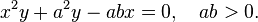Serpentine curve
For serpentine shapes in architecture and design, see Serpentine shape.
A serpentine curve is a curve whose equation is of the form
Equivalently, it has a parametric representation
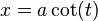 ,
, 
or functional representation
History
Serpentine curves were studied by L'Hôpital and Huygens, and named and classified by Newton.
Visual appearance

The serpentine curve for a = b = 1.
External links
This article is issued from Wikipedia - version of the Saturday, March 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.