Semi-simplicity
In mathematics, semi-simplicity is a widespread concept in disciplines such as linear algebra, abstract algebra, representation theory, category theory and algebraic geometry. A semi-simple object is one that can be decomposed into a sum of simple objects, and simple objects are those which do not contain non-trivial sub-objects. The precise definitions of these words depends on the context.
For example, if G is a finite group, then a nontrivial finite-dimensional representation V over a field is said to be simple if the only subrepresentations it contains are either {0} or V (these are also called irreducible representations). Then Maschke's theorem says that any finite-dimensional representation is a direct sum of simple representations (provided the characteristic does not divide the order of the group). So, in this case, every representation of a finite group is semi-simple. Especially in algebra and representation theory, "semi-simplicity" is also called complete reducibility. For example, Weyl's theorem on complete reducibility says a finite-dimensional representation of a semisimple compact Lie group is semisimple.
A square matrix (in other words a linear operator 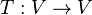 with V finite dimensional vector space) is said to be simple if the only subspaces which are invariant under T are {0} and V. If the field is algebraically closed (such as the complex numbers), then the only simple matrices are of size 1 by 1. A semi-simple matrix is one that is similar to a direct sum of simple matrices; if the field is algebraically closed, this is the same as being diagonalizable.
with V finite dimensional vector space) is said to be simple if the only subspaces which are invariant under T are {0} and V. If the field is algebraically closed (such as the complex numbers), then the only simple matrices are of size 1 by 1. A semi-simple matrix is one that is similar to a direct sum of simple matrices; if the field is algebraically closed, this is the same as being diagonalizable.
These notions of semi-simplicity can be unified using the language of semi-simple modules, and generalized to semi-simple categories.
Introductory example of vector spaces
If one considers all vector spaces (over a field, such as the real numbers), the simple vector spaces are those which contain no proper subspaces. Therefore, the one-dimensional vector spaces are the simple ones. So it is a basic result of linear algebra that any finite-dimensional vector space is the direct sum of simple vector spaces; in other words, all finite-dimensional vector spaces are semi-simple.
Semi-simple modules and rings
For a fixed ring R, a nontrivial R-module M is simple, if it has no submodules other than 0 and M. An R-module M is semi-simple if every R-submodule of M is an R-module direct summand of M (the trivial module 0 is semi-simple, but not simple). For an R-module M, M is semi-simple if and only if it is the direct sum of simple modules (the trivial module is the empty direct sum). Finally, R is called a semi-simple ring if it is semi-simple as an R-module. As it turns out, this is equivalent to requiring that any finitely generated R-module M is semi-simple.[1]
Examples of semi-simple rings include fields and, more generally, finite direct products of fields. For a finite group G Maschke's theorem asserts that the group ring R[G] over some ring R is semi-simple if and only if R is semi-simple and |G| is invertible in R. Since the theory of modules of R[G] is the same as the representation theory of G on R-modules, this fact is an important dichotomy, which causes modular representation theory, i.e., the case when |G| does divide the characteristic of R to be more difficult than the case when |G| does not divide the characteristic, in particular if R is a field of characteristic zero.
By the Artin–Wedderburn theorem, a unital Artinian ring R is semisimple if and only if it is (isomorphic to) 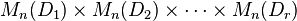 , where each
, where each 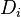 is a division ring and
is a division ring and  is the ring of n-by-n matrices with entries in D.
is the ring of n-by-n matrices with entries in D.
As indicated above, the theory of semi-simple rings is much more easy than the one of general rings. For example, any short exact sequence
of modules over a semi-simple ring must split, i.e., 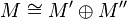 . From the point of view of homological algebra, this means that there are no non-trivial extensions. The ring Z of integers is not semi-simple: Z is not the direct sum of nZ and Z/n.
. From the point of view of homological algebra, this means that there are no non-trivial extensions. The ring Z of integers is not semi-simple: Z is not the direct sum of nZ and Z/n.
Semi-simple matrices
A matrix or, equivalently, a linear operator T on a finite-dimensional vector space V is called semi-simple if every T-invariant subspace has a complementary T-invariant subspace.[2][3] This is equivalent to the minimal polynomial of T being square-free.
For vector spaces over an algebraically closed field F, semi-simplicity of a matrix is equivalent to diagonalizability.[2] This is because such an operator always has an eigenvector; if it is, in addition, semi-simple, then it has a complementary invariant hyperplane, which itself has an eigenvector, and thus by induction is diagonalizable. Conversely, diagonalizable operators are easily seen to be semi-simple, as invariant subspaces are direct sums of eigenspaces, and any basis for this space can be extended to an eigenbasis.
Actually this notion of semi-simplicity is a special case of the one of rings: T is semi-simple if and only if the subalgebra ![F[T] \subset \operatorname{End}_F(V)](../I/m/eeaf7150405f09a2c5ca74674eb3c7b4.png) generated by the powers (i.e., iterations) of T inside the ring of endomorphisms of V is semi-simple.
generated by the powers (i.e., iterations) of T inside the ring of endomorphisms of V is semi-simple.
Semi-simple categories
Many of the above notions of semi-simplicity are recovered by the concept of a semi-simple category C. Briefly, a category is a collection of objects and maps between such objects, the idea being that the maps between the objects preserve some structure inherent in these objects. For example, R-modules and R-linear maps between them form a category, for any ring R.
An abelian category[4] C is called semi-simple if there is a collection of simple objects 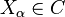 , i.e., ones which have no subobject other than the zero object 0 and
, i.e., ones which have no subobject other than the zero object 0 and 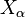 itself, such that any object X is the direct sum (i.e., coproduct or, equivalently, product) of simple objects.
itself, such that any object X is the direct sum (i.e., coproduct or, equivalently, product) of simple objects.
With this terminology, a ring R is semi-simple if and only if the category of finitely generated R-modules is semisimple.
An example from Hodge theory is the category of polarizable pure Hodge structures, i.e., pure Hodge structures equipped with a suitable positive definite bilinear. The presence of this so-called polarization causes the category of polarizable Hodge structures to be semi-simple.[5]
Another example from algebraic geometry is the category of pure motives of smooth projective varieties over a field k 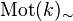 modulo an adequate equivalence relation
modulo an adequate equivalence relation  . As was conjectured by Grothendieck and shown by Jannsen, this category is semi-simple if and only if the equivalence relation is numerical equivalence.[6] This fact is a conceptual cornerstone in the theory of motives.
. As was conjectured by Grothendieck and shown by Jannsen, this category is semi-simple if and only if the equivalence relation is numerical equivalence.[6] This fact is a conceptual cornerstone in the theory of motives.
Semi-simplicity in representation theory
One can ask whether the category of (say, finite-dimensional) representations of a group G is semisimple or not (in such a category, irreducible representations are precisely simple objects). For example, the category is semisimple if G is a semisimple compact Lie group (Weyl's theorem on complete reducibility).
See also: fusion category (which is semisimple).
See also
- A semisimple Lie algebra is a Lie algebra that is a direct sum of simple Lie algebras.
- A semisimple algebraic group is a linear algebraic group whose radical of the identity component is trivial.
- Semisimple algebra
References
- ↑
- Lam, Tsit-Yuen (2001). A first course in noncommutative rings. Graduate texts in mathematics 131 (2 ed.). Springer. ISBN 0-387-95183-0.
- 1 2 Lam (2001), p. 39
- ↑ Hoffman, Kenneth; Kunze, Ray (1971). "Semi-Simple operators". Linear algebra (2nd ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc. MR 0276251.
- ↑ More generally, the same definition of semi-simplicity works for pseudo-abelian additive categories. See for example Yves André, Bruno Kahn: Nilpotence, radicaux et structures monoïdales. With an appendix by Peter O'Sullivan. Rend. Sem. Mat. Univ. Padova 108 (2002), 107–291. http://arxiv.org/abs/math/0203273.
- ↑ Peters, Chris A. M.; Steenbrink, Joseph H. M. Mixed Hodge structures. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 52. Springer-Verlag, Berlin, 2008. xiv+470 pp. ISBN 978-3-540-77015-2; see Corollary 2.12
- ↑ Uwe Jannsen: Motives, numerical equivalence, and semi-simplicity, Invent. math. 107, 447~452 (1992)
External links
- http://mathoverflow.net/questions/245/are-abelian-nondegenerate-tensor-categories-semisimple
- http://ncatlab.org/nlab/show/semisimple+category
