Seminormal ring

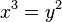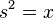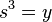In algebra, a seminormal ring is a commutative reduced ring in which, whenever x, y satisfy $x^3 = y^2$ , there is s with $s^2 = x$ and $s^3 = y$ . This definition was given by Swan (1980) as a simplification of the original definition of Traverso (1970). A basic example is an integrally closed domain.

A semigroup is said to be seminormal if its semigroup algebra is seminormal.

References

Swan, Richard G. (1980), "On seminormality", Journal of Algebra 67 (1): 210–229, doi:10.1016/0021-8693(80)90318-X, ISSN 0021-8693, MR 595029
Traverso, Carlo (1970), "Seminormality and Picard group", Ann. Scuola Norm. Sup. Pisa (3) 24: 585–595, MR 0277542
Vitulli, Marie A. (2011), "Weak normality and seminormality", Commutative algebra---Noetherian and non-Noetherian perspectives (PDF), Berlin, New York: Springer-Verlag, pp. 441–480, doi:10.1007/978-1-4419-6990-3_17, MR 2762521
Charles Weibel, The K-book: An introduction to algebraic K-theory

This article is issued from Wikipedia - version of the Friday, April 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.