Hereditary ring

In mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective. If this is required only for finitely generated submodules, it is called semihereditary.

For a noncommutative ring R, the terms left hereditary and left semihereditary and their right hand versions are used to distinguish the property on a single side of the ring. To be left (semi-)hereditary, all (finitely generated) submodules of projective left R-modules must be projective, and to be right (semi-)hereditary all (finitely generated) submodules of projective right submodules must be projective. It is possible for a ring to be left (semi-)hereditary but not right (semi-)hereditary, and vice versa.

Equivalent definitions

The ring R is left (semi-)hereditary if and only if all (finitely generated) left ideals of R are projective modules.^[1]^[2]
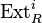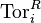The ring R is left hereditary if and only if all left modules have projective resolutions of length at most 1. This is equivalent to saying that the left global dimension is at most 1. Hence the usual derived functors such as $\mathrm{Ext}_R^i$ and $\mathrm{Tor}_i^R$ are trivial for $i>1$ .

Examples

Semisimple rings are easily seen to be left and right hereditary via the equivalent definitions: all left and right ideals are summands of R, and hence are projective. By a similar token, in a von Neumann regular ring every finitely generated left and right ideal is a direct summand of R, and so von Neumann regular rings are left and right semihereditary.

For any nonzero element x in a domain R, 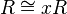$R\cong xR$ via the map 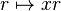$r\mapsto xr$ . Hence in any domain, a principal right ideal is free, hence projective. This reflects the fact that domains are right Rickart rings. It follows that if R is a right Bézout domain, so that finitely generated right ideals are principal, then R has all finitely generated right ideals projective, and hence R is right semihereditary. Finally if R is assumed to be a principal right ideal domain, then all right ideals are projective, and R is right hereditary.

A commutative hereditary integral domain is called a Dedekind domain. A commutative semi-hereditary integral domain is called a Prüfer domain.

An important example of a (left) hereditary ring is the path algebra of a quiver. This is a consequence of the existence of the standard resolution (which is of length 1) for modules over a path algebra.

The triangular matrix ring $\begin{bmatrix}Z&Q \\0&Q \end{bmatrix}$ is right hereditary and left semi-hereditary but not left hereditary.

If S is a von Neumann regular ring with an ideal I that is not a direct summand, then the triangular matrix ring 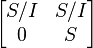$\begin{bmatrix}S/I&S/I \\0&S \end{bmatrix}$ is left semi-hereditary but not right semi-hereditary.

Properties

For a left hereditary ring R, every submodule of a free left R-module is isomorphic to a direct sum of left ideals of R and hence is projective.^[2]

References

↑ Lam 1999, p. 42
1 2 Reiner 2003, pp. 27–29

Crawley-Boevey, William, Notes on Quiver Representation (PDF)
Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294, Zbl 0911.16001
Osborne, M. Scott (2000), Basic Homological Algebra, Graduate Texts in Mathematics 196, Springer-Verlag, ISBN 0-387-98934-X, Zbl 0948.18001
Reiner, I. (2003), Maximal Orders, London Mathematical Society Monographs. New Series 28, Oxford University Press, ISBN 0-19-852673-3, Zbl 1024.16008
Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge: Cambridge University Press, ISBN 0-521-43500-5, Zbl 0797.18001

This article is issued from Wikipedia - version of the Friday, January 29, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.