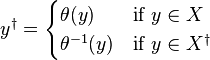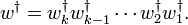Semigroup with involution

In mathematics, particularly in abstract algebra, a semigroup with involution or a *-semigroup is a semigroup equipped with an involutive anti-automorphism, which—roughly speaking—brings it closer to a group because this involution, considered as unary operator, exhibits certain fundamental properties of the operation of taking the inverse in a group: uniqueness, double application "cancelling itself out", and the same interaction law with the binary operation as in the case of the group inverse. It is thus not a surprise that any group is a semigroup with involution. However, there are significant natural examples of semigroups with involution that are not groups.

An example from linear algebra is the multiplicative monoid of real square matrices of order n (called the full linear monoid). The map which sends a matrix to its transpose is an involution because the transpose is well defined for any matrix and obeys the law (AB)T = BTAT which has the same form of interaction with multiplication as taking inverses has in the general linear group (which is a subgroup of the full linear monoid). However, for an arbitrary matrix AAT does not equal the identity element (namely the diagonal matrix). Another example, coming from formal language theory, is the free semigroup generated by a nonempty set (an alphabet), with string concatenation as the binary operation, and the involution being the map which reverses the linear order of the letters in a string. A third example, from basic set theory, is the set of all binary relations between a set and itself, with the involution being the inverse relation, and the multiplication given by the usual composition of relations.

Semigroups with involution appeared explicitly named in a 1953 paper of Viktor Wagner (in Russian) as result of his attempt to bridge the theory of semigroups with that of semiheaps.[1]

Formal definition

Let S be a semigroup with its binary operation written multiplicatively. An involution in S is a unary operation * on S (or, a transformation * : S → S, x ↦ x*) satisfying the following conditions:

  1. For all x in S, (x*)* = x.
  2. For all x, y in S we have (xy)* = y*x*.

The semigroup S with the involution * is called a semigroup with involution.

Semigroups that satisfy only the first of these axioms belong to the larger class of U-semigroups.

In some applications, the second of these axioms has been called antidistributive.[2] Regarding the natural philosophy of this axiom, H.S.M. Coxeter remarked that it "becomes clear when we think of [x] and [y] as the operations of putting on our socks and shoes, respectively."[3]

Examples

  1. If S is a commutative semigroup then the identity map of S is an involution.
  2. If S is a group then the inversion map * : S → S defined by x* = x−1 is an involution. Furthermore, on an abelian group both this map and the one from the previous example are involutions satisfying the axioms of semigroup with involution.[4]
  3. If S is an inverse semigroup then the inversion map is an involution which leaves the idempotents invariant. As noted in the previous example, the inversion map is not necessarily the only map with this property in an inverse semigroup; there may well be other involutions that leave all idempotents invariant; for example the identity map on a commutative regular, hence inverse, semigroup, in particular, an abelian group. A regular semigroup is an inverse semigroup if and only if it admits an involution under which each idempotent is an invariant.[5]
  4. Underlying every C*-algebra is a *-semigroup. An important instance is the algebra Mn(C) of n-by-n matrices over C, with the conjugate transpose as involution.
  5. If X is a set, the set of all binary relations on X is a *-semigroup with the * given by the inverse relation, and the multiplication given by the usual composition of relations. This is an example of a *-semigroup which is not a regular semigroup.
  6. If X is a set, then the set of all finite sequences (or strings) of members of X forms a free monoid under the operation of concatenation of sequences, with sequence reversal as an involution.
  7. A rectangular band on a Cartesian product of a set A with itself, i.e. with elements from A × A, with the semigroup product defined as (a, b)(c, d) = (a, d), with the involution being the order reversal of the elements of a pair (a, b)* = (b, a). This semigroup is also a regular semigroup, as all bands are.[6]

Basic concepts and properties

An element x of a semigroup with involution is sometimes called hermitian (by analogy with a Hermitian matrix) when it is left invariant by the involution, meaning x* = x. Elements of the form xx* or x*x are always hermitian, and so are all powers of a hermitian element. As noted in the examples section, a semigroup S is an inverse semigroup if and only if S is a regular semigroup and admits an involution such that every idempotent is hermitian.[7]

Certain basic concepts may be defined on *-semigroups in a way that parallels the notions stemming from a regular element in a semigroup. A partial isometry is an element s such that ss*s = s; the set of partial isometries of a semigroup S is usually abbreviated PI(S).[8] A projection is an idempotent element e that is also hermitian, meaning that ee = e and e* = e. Every projection is a partial isometry, and for every partial isometry s, s*s and ss* are projections. If e and f are projections, then e = ef if and only if e = fe.[9]

Partial isometries can be partially ordered by s ≤ t defined as holding whenever s = ss*t and ss* = ss*tt*.[9] Equivalently, s ≤ t if and only if s = et and e = ett* for some projection e.[9] In a *-semigroup, PI(S) is an ordered groupoid with the partial product given by s⋅t = st if s*s = tt*.[10]

Examples

In terms of examples for these notions, in the *-semigroup of binary relations on a set, the partial isometries are the relations that are difunctional. The projections in this *-semigroup are the partial equivalence relations.[11]

The partial isometries in a C*-algebra are exactly those defined in this section. In the case of Mn(C) more can be said. If E and F are projections, then E ≤ F if and only if imE ⊆ imF. For any two projection, if E ∩ F = V, then the unique projection J with image V and kernel the orthogonal complement of V is the meet of E and F. Since projections form a meet-semilattice, the partial isometries on Mn(C) form an inverse semigroup with the product A(A^*A\wedge BB^*)B.[12]

Another simple example of these notions appears in the next section.

Notions of regularity

There two related, but not identical notions of regularity in *-semigroups. They were introduced nearly simultaneously by Nordahl & Scheiblich (1978) and respectively Drazin (1979).[13]

Regular *-semigroups (Nordahl & Scheiblich)

As mentioned in the previous examples, inverse semigroups are a subclass *-semigroups. It is also textbook knowledge that an inverse semigroup can be characterized as a regular semigroup in which any two idempotents commute. In 1963, Boris M. Schein has published the following two axioms providing an analogous characterization of inverse semigroups as a subvariety of *-semigroups:

The first of these looks like the definition of a regular element, but is actually in terms of the involution. Likewise, the second axiom appears to be describing the commutation of two idempotents. It is known however that regular semigroups do not form a variety because their class does not contain free objects (a result established by D. B. McAlister in 1968). This line of reasoning motivated Nordahl and Scheiblich to begin in 1977 the study of the (variety of) *-semigroups that satisfy only the first these two axioms; because of the similarity in form with the property defining regular semigroups, they named this variety regular *-semigroups.

It is a simple calculation to establish that a regular *-semigroup is also a regular semigroup because x* turns out to be an inverse of x. The rectangular band from example 7 is a regular *-semigroup that is not an inverse semigroup.[6] It is also easy to verify that in a regular *-semigroup the product of any two projections is an idempotent.[14] In the aforementioned rectangular band example, the projections are elements of the form (x, x) and [like all elements of a band] are idempotent. However, two different projections in this band need not commute, nor is their product necessarily a projection since (a, a)(b, b) = (a, b).

Semigroups that satisfy only x** = x = xx*x (but not necessarily the antidistributivity of * over multiplication) have also been studied under the name of I-semigroups.

P-systems

The problem of characterizing when a regular semigroup is a regular *-semigroup (in the sense of Nordahl & Scheiblich) was addressed by M. Yamada (1982). He defined a P-system F(S) as subset of the idempotents of S, denoted as usual by E(S). Using the usual notation V(a) for the inverses of a, F(S) needs to satisfy the following axioms:

  1. For any a in S, there exists a unique a° in V(a) such that aa° and a°a are in F(S)
  2. For any a in S, and b in F(S), a°ba is in F(S), where ° is the well-defined operation from the previous axiom
  3. For any a, b in F(S), ab is in E(S); note: not necessarily in F(S)

A regular semigroup S is a *-regular semigroup, as defined by Nordahl & Scheiblich, if and only if it has a p-system F(S). In this case F(S) is the set of projections of S with respect to the operation ° defined by F(S). In an inverse semigroup the entire semilattice of idempotents is a p-system. Also, if a regular semigroup S has a p-system that is multiplicatively closed (i.e. subsemigroup), then S is an inverse semigroup. Thus, a p-system may be regarded as a generalization of the semilattice of idempotents of an inverse semigroup.

*-regular semigroups (Drazin)

A semigroup S with an involution * is called a *-regular semigroup (in the sense of Drazin) if for every x in S, x* is H-equivalent to some inverse of x, where H is the Green’s relation H. This defining property can be formulated in several equivalent ways. Another is to say that every L-class contains a projection. An axiomatic definition is the condition that for every x in S there exists an element x′ such that x′xx′ = x′, xx′x = x, (xx′)* = xx′, (x′x)* = x′x. Michael P. Drazin first proved that given x, the element x′ satisfying these axioms is unique. It is called the Moore–Penrose inverse of x. This agrees with the classical definition of the Moore–Penrose inverse of a square matrix. In the multiplicative semigroup Mn ( C ) of square matrices of order n, the map which assigns a matrix A to its Hermitian conjugate A* is an involution. The semigroup Mn ( C ) is a *-regular semigroup with this involution. The Moore–Penrose inverse of A in this *-regular semigroup is the classical Moore–Penrose inverse of A.

Free semigroup with involution

As with all varieties, the category of semigroups with involution admits free objects. The construction of a free semigroup (or monoid) with involution is based on that of a free semigroup (and respectively that of a free monoid). Moreover, the construction of a free group can easily be derived by refining the construction of a free monoid with involution.[15]

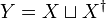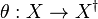The generators of a free semigroup with involution are the elements of the union of two (equinumerous) disjoint sets in bijective correspondence: Y=X\sqcup X^\dagger. 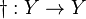(Here the notation \sqcup\, emphasized that the union is actually a disjoint union.) In the case were the two sets are finite, their union Y is sometimes called an alphabet with involution[16] or a symmetric alphabet.[17] Let \theta:X\rightarrow X^\dagger be a bijection; \theta is naturally extended to a bijection { }\dagger: Y \to Y essentially by taking the disjoint union of \theta (as a set) with its inverse, or in piecewise notation:[18]

y^\dagger = \begin{cases} \theta(y) & \text{if } y \in X \\ \theta^{-1}(y) & \text{if } y \in X^\dagger \end{cases}

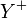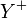Now construct Y^+\, as the free semigroup on Y\, in the usual way with the binary (semigroup) operation on Y^+\, being concatenation:

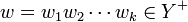w = w_1w_2 \cdots w_k \in Y^+ for some letters w_i\in Y.

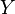The bijection \dagger on Y is then extended as a bijection 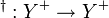{ }^\dagger:Y^+\rightarrow Y^+ defined as the string reversal of the elements of 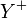Y^+\, that consist of more than one letter:[16][18]

w^\dagger=w_k^\dagger w_{k-1}^\dagger \cdots w_{2}^\dagger w_{1}^\dagger.

This map is an involution on the semigroup 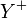Y^+\,. Thus, the semigroup 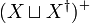(X\sqcup X^\dagger)^+ with the map 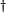{ }^\dagger\, is a semigroup with involution, called a free semigroup with involution on X.[19] (The irrelevance of the concrete identity of 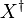X^\dagger and of the bijection \theta in this choice of terminology is explained below in terms of the universal property of the construction.) Note that unlike in example 6, the involution of every letter is a distinct element in an alphabet with involution, and consequently the same observation extends to a free semigroup with involution.

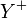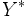If in the above construction instead of Y^+\, we use the free monoid Y^*=Y^+\cup\{\varepsilon\}, which is just the free semigroup extended with the empty word \varepsilon\, (which is the identity element of the monoid Y^*\,), and suitably extend the involution with \varepsilon^\dagger = \varepsilon, we obtain a free monoid with involution.[18]

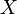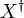The construction above is actually the only way to extend a given map \theta\, from X\, to X^\dagger\,, to an involution on 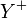Y^+\, (and likewise on 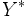Y^*\,). The qualifier "free" for these constructions is justified in the usual sense that they are universal constructions. 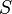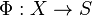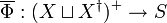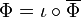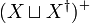In the case of the free semigroup with involution, given an arbitrary semigroup with involution S\, and a map \Phi:X\rightarrow S, then a semigroup homomorphism \overline\Phi:(X\sqcup X^\dagger)^+\rightarrow S exists such that \Phi = \iota \circ \overline\Phi, where \iota : X \rightarrow (X\sqcup X^\dagger)^+ is the inclusion map and composition of functions is taken in diagram order.[19] The construction of (X\sqcup X^\dagger)^+ as a semigroup with involution is unique up to isomorphism. An analogous argument holds for the free monoid with involution in terms of monoid homomorphisms and the uniqueness up to isomorphism of the construction of (X\sqcup X^\dagger)^* as a monoid with involution.

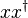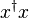The construction of a free group is not very far off from that of a free monoid with involution. The additional ingredient needed is to define a notion of reduced word and a rewriting rule for producing such words simply by deleting any adjacent pairs of letter of the form xx^\dagger or x^\dagger x. It can be shown than the order of rewriting (deleting) such pairs does not matter, i.e. any order of deletions produces the same result.[15] (Otherwise put it, these rules define a confluent rewriting system.) Equivalently, a free group is constructed from a free monoid with involution by taking the quotient of the latter by the congruence \{ (yy^\dagger, \varepsilon) : y\in Y\}, which is sometimes called the Dyck congruence—in a certain sense it generalizes Dyck language to multiple kinds of "parantheses", however simplification in the Dyck congruence takes place regardless of order, e.g. 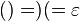if ")" is the inverse of "(", then ()=)(=\varepsilon; the one-sided congruence that appears in the Dyck language proper 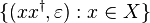\{ (xx^\dagger, \varepsilon) : x\in X\}, which instantiates only to 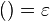()=\varepsilon is (perhaps confusingly) called the Shamir congruence. The quotient of a free monoid with involution by the Shamir congruence is not a group, but a monoid ; nevertheless it has been called the free half group by its first discoverer—Eli Shamir— although more recently it has been called the involutive monoid generated by X.[17][20] (This latter choice of terminology conflicts however with the use of "involutive" to denote any semigroup with involution— a practice also encountered in the literature.[21][22])

Baer *-semigroups

A Baer *-semigroup is a *-semigroup with (two-sided) zero in which the right annihilator of every element coincides with the right ideal of some projection; this property is expressed formally as: for all x ∈ S there exists a projection e such that

{ y ∈ S | xy = 0 } = eS.[22]

The projection e is in fact uniquely determined by x.[22]

More recently, Baer *-semigroups have been also called Foulis semigroups, after David James Foulis who studied them in depth.[23][24]

Examples and applications

The set of all binary relations on a set (from example 5) is a Baer *-semigroup.[25]

Baer *-semigroups are also encountered in quantum mechanics,[22] in particular as the multiplicative semigroups of Baer *-rings.

If H is a Hilbert space, then the multiplicative semigroup of all bounded operators on H is a Baer *-semigroup. The involution in this case maps an operator to its adjoint.[25]

Baer *-semigroup allow the coordinatization of orthomodular lattices.[23]

See also

Notes

  1. ↑ Christopher Hollings (2014). Mathematics across the Iron Curtain: A History of the Algebraic Theory of Semigroups. American Mathematical Society. p. 265. ISBN 978-1-4704-1493-1.
  2. ↑ Chris Brink; Wolfram Kahl; Gunther Schmidt (1997). Relational Methods in Computer Science. Springer. p. 4. ISBN 978-3-211-82971-4.
  3. ↑ H.S.M. Coxeter, Introduction to Geometry, p. 33
  4. ↑ C. van den Berg; J. P. R. Christensen; P. Ressel (2012). Harmonic Analysis on Semigroups: Theory of Positive Definite and Related Functions. Springer Science & Business Media. pp. 87–88. ISBN 978-1-4612-1128-0.
  5. ↑ Munn, Lemma 1
  6. 1 2 Nordahl and Scheiblich
  7. ↑ Easdown, David, and W. D. Munn. "On semigroups with involution." Bulletin of the Australian Mathematical Society 48.01 (1993): 93-100.
  8. ↑ Lawson, p. 116
  9. 1 2 3 Lawson, p. 117
  10. ↑ Lawson, p. 118
  11. ↑ Lawson p.122 and p.35
  12. ↑ Lawson p.120
  13. ↑ Crvenkovic and Dolinka
  14. ↑ Nordahl and Scheiblich, Theorem 2.5
  15. 1 2 Lawson p. 51
  16. 1 2 Andrzej Ehrenfeucht; T. Harju; Grzegorz Rozenberg (1999). The Theory of 2-structures: A Framework for Decomposition and Transformation of Graphs. World Scientific. pp. 13–14. ISBN 978-981-02-4042-4.
  17. 1 2 Jacques Sakarovitch. Elements of Automata Theory. Cambridge University Press. pp. 305–306.
  18. 1 2 3 Stephen Lipscomb (1996). Symmetric Inverse Semigroups. American Mathematical Soc. p. 86. ISBN 978-0-8218-0627-2.
  19. 1 2 Lawson p. 172
  20. ↑ Ion Petre and Arto Salomaa (2009). "Algebraic Systems and Pushdown Automata". In Manfred Droste, Werner Kuich, Heiko Vogler. Handbook of Weighted Automata. Springer. p. 271. ISBN 978-3-642-01492-5.
  21. ↑ Karl-Hermann Neeb (2000). Holomorphy and Convexity in Lie Theory. Walter de Gruyter. p. 21. ISBN 978-3-11-015669-0.
  22. 1 2 3 4 Enrico G. Beltrametti; Gianni Cassinelli (2010) [1981]. The Logic of Quantum Mechanics. Cambridge University Press. p. 178. ISBN 978-0-521-16849-6.
  23. 1 2 T.S. Blyth (2006). Lattices and Ordered Algebraic Structures. Springer Science & Business Media. pp. 101–102. ISBN 978-1-84628-127-3.
  24. ↑ Harding, John. “Daggers, Kernels, Baer *-Semigroups, and Orthomodularity.” Journal of Philosophical Logic. April 6, 2013. doi:10.1007/s10992-013-9275-5
  25. 1 2 Foulis, D. J. Relative inverses in Baer *-semigroups. Michigan Math. J. 10 (1963), no. 1, 65--84. doi:10.1307/mmj/1028998825.

References

This article is issued from Wikipedia - version of the Monday, December 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.