Semi-invariant of a quiver
In mathematics, given a quiver Q with set of vertices Q0 and set of arrows Q1, a representation of Q assigns a vector space Vi to each vertex and a linear map V(α): V(s(α)) → V(t(α)) to each arrow α, where s(α), t(α) are, respectively, the starting and the ending vertices of α. Given an element d ∈ ℕQ0, the set of representations of Q with dim Vi = d(i) for each i has a vector space structure.
It is naturally endowed with an action of the algebraic group ∏i∈ Q0 GL(d(i)) by simultaneous base change. Such action induces one on the ring of functions. The ones which are invariants up to a character of the group are called semi-invariants. They form a ring whose structure reflects representation-theoretical properties of the quiver.
Definitions
Let Q = (Q0,Q1,s,t) be a quiver. Consider a dimension vector d, that is an element in ℕQ0. The set of d-dimensional representations is given by
Once fixed bases for each vector space Vi this can be identified with the vector space
Such affine variety is endowed with an action of the algebraic group GL(d) := ∏i∈ Q0 GL(d(i)) by simultaneous base change on each vertex:
By definition two modules M,N ∈ Rep(Q,d) are isomorphic if and only if their GL(d)-orbits coincide.
We have an induces action on the coordinate ring k[Rep(Q,d)] by defining:
Polynomial invariants
An element f ∈ k[Rep(Q,d)] is called an invariant (with respect to GL(d)) if g⋅f = f for any g ∈ GL(d). The set of invariants
is in general a subalgebra of k[Rep(Q,d)].
Example
Consider the 1-loop quiver Q:
For d = (n) the representation space is End(kn) and the action of GL(n) is given by usual conjugation. The invariant ring is
where the cis are defined, for any A ∈ End(kn), as the coefficients of the characteristic polynomial
Semi-invariants
In case Q has neither loops nor cycles the variety k[Rep(Q,d)] has a unique closed orbit corresponding to the unique d-dimensional semi-simple representation, therefore any invariant function is constant.
Elements which are invariants with respect to the subgroup SL(d) := ∏{i ∈ Q0} SL(d(i)) form a ring, SI(Q,d), with a richer structure called ring of semi-invariants. It decomposes as
where
A function belonging to SI(Q,d)σ is called semi-invariant of weight σ.
Example
Consider the quiver Q:
Fix d = (n,n). In this case k[Rep(Q,(n,n))] is congruent to the set of square matrices of size n: M(n). The function defined, for any B ∈ M(n), as detu(B(α)) is a semi-invariant of weight (u,−u) in fact
The ring of semi-invariants equals the polynomial ring generated by det, i.e.
Characterization of representation type through semi-invariant theory
For quivers of finite representation-type, that is to say Dynkin quivers, the vector space k[Rep(Q,d)] admits an open dense orbit. In other words, it is a prehomogenous vector space. Sato and Kimura described the ring of semi-invariants in such case.
Sato–Kimura theorem
Let Q be a Dynkin quiver, d a dimension vector. Let ∑ be the set of weights σ such that there exists fσ ∈ SI(Q,d)σ non-zero and irreducible. Then the following properties hold true.
i) For every weight σ we have dimk SI(Q,d)σ ≤ 1.
ii) All weights in ∑ are linearly independent over ℚ.
iii) SI(Q,d) is the polynomial ring generated by the fσ's, σ ∈ ∑.
Furthermore, we have an interpretation for the generators of this polynomial algebra. Let O be the open orbit, then k[Rep(Q,d)] \ O = Z1 ∪ ... ∪ Zt where each Zi is closed and irreducible. We can assume that the Zis are arranged in increasing order with respect to the codimension so that the first l have codimension one and Zi is the zero-set of the irreducible polynomial f1, then SI(Q,d) = k[f1, ..., fl].
Example
In the example above the action of GL(n,n) has an open orbit on M(n) consisting of invertible matrices. Then we immediately recover SI(Q,(n,n)) = k[det].
Skowronski–Weyman provided a geometric characterization of the class of tame quivers (i.e. Dynkin and Euclidean quivers) in terms of semi-invariants.
Skowronski–Weyman theorem
Let Q be a finite connected quiver. The following are equivalent:
i) Q is either a Dynkin quiver or an Euclidean quiver.
ii) For each dimension vector d, the algebra SI(Q,d) is complete intersection.
iii) For each dimension vector d, the algebra SI(Q,d) is either a polynomial algebra or a hypersurface.
Example
Consider the Euclidean quiver Q:
Pick the dimension vector d = (1,1,1,1,2). An element V ∈ k[Rep(Q,d)] can be identified with a 4-ple (A1, A2, A3, A4) of matrices in M(1,2). Call Di,j the function defined on each V as det(Ai,Aj). Such functions generate the ring of semi-invariants:
References
- Derksen, H.; Weyman, J. (2000), "Semi-invariants of quivers and saturation for Littlewood–Richardson coefficients.", J. Amer. Math. Soc. 3 (13): 467–479, MR 1758750
- Sato, M.; Kimura, T. (1977), "A classification of irreducible prehomogeneous vector spaces and their relative invariants.", Nagoya Math. J. 65: 1–155, MR 0430336
- Skowronski, A.; Weyman, J. (2000), "The algebras of semi-invariants of quivers.", Transform. Groups 5 (4): 361–402, doi:10.1007/bf01234798, MR 1800533
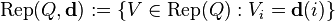
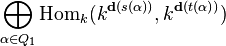
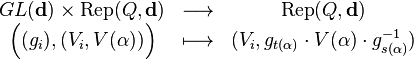
![\begin{array}{ccc}
GL(\mathbf{d}) \times k[\operatorname{Rep}(Q,\mathbf{d})] & \longrightarrow & k[\operatorname{Rep}(Q,\mathbf{d})]\\
(g, f) & \longmapsto & g\cdot f(-):=f(g^{-1}. -)
\end{array}](../I/m/57b20dd87a5170bd3c2106cd2630d186.png)
![I(Q,\mathbf{d}):=k[\operatorname{Rep}(Q,\mathbf{d})]^{GL(\mathbf{d})}](../I/m/c506cb28ca54d70885fabee69da86a9f.png)

![I(Q,\mathbf{d})=k[c_1,\ldots,c_n]](../I/m/a5a1cc92a317749c9af108adab150816.png)
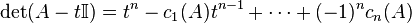
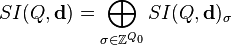
![SI(Q,\mathbf{d})_{\sigma}:= \{f\in k[\operatorname{Rep}(Q,\mathbf{d})] : g\cdot f = \prod_{i\in Q_0}\det(g_i)^{\sigma_i} f, \forall g\in GL(\mathbf{d})\}.](../I/m/984d85cd1cbae3602b79a922a7abf441.png)
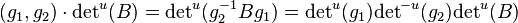
![\mathsf{SI}(Q,\mathbf{d})=k[\det]](../I/m/ed4a0fcb90e3b9d621afb87cc2476f6b.png)

![SI(Q,\mathbf{d})=\frac{k[D_{1,2},D_{3,4},D_{1,4},D_{2,3},D_{1,3},D_{2,4}]}{D_{1,2}D_{3,4}+D_{1,4}D_{2,3}-D_{1,3}D_{2,4}}](../I/m/3a802b82ac601ac7599e381f59a9f46c.png)