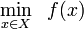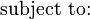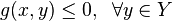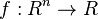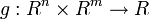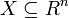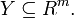Semi-infinite programming

In optimization theory, semi-infinite programming (SIP) is an optimization problem with a finite number of variables and an infinite number of constraints, or an infinite number of variables and a finite number of constraints. In the former case the constraints are typically parameterized.[1]

Mathematical formulation of the problem

The problem can be stated simply as:

\min_{x \in X}\;\; f(x)
\text{subject to: }\
g(x,y) \le 0, \;\; \forall y \in Y

where

f: R^n \to R
g: R^n \times R^m \to R
X \subseteq R^n
Y \subseteq R^m.

SIP can be seen as a special case of bilevel programs in which the lower-level variables do not participate in the objective function.

Methods for solving the problem

In the meantime, see external links below for a complete tutorial.

Examples

In the meantime, see external links below for a complete tutorial.

See also

References

  1. ↑
    • Bonnans, J. Frédéric; Shapiro, Alexander (2000). "5.4 and 7.4.4 Semi-infinite programming". Perturbation analysis of optimization problems. Springer Series in Operations Research. New York: Springer-Verlag. pp. 496–526 and 581. ISBN 0-387-98705-3. MR 1756264.
    • M. A. Goberna and M. A. López, Linear Semi-Infinite Optimization, Wiley, 1998.
    • Hettich, R.; Kortanek, K. O. (1993). "Semi-infinite programming: Theory, methods, and applications". SIAM Review 35 (3). pp. 380–429. doi:10.1137/1035089. JSTOR 2132425. MR 1234637.

External links


This article is issued from Wikipedia - version of the Monday, August 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.