Semantics encoding
A semantics encoding is a translation between formal languages. For programmers, the most familiar form of encoding is the compilation of a programming language into machine code or byte-code. Conversion between document formats are also forms of encoding. Compilation of TeX or LaTeX documents to PostScript are also commonly encountered encoding processes. Some high-level preprocessors such as OCaml's Camlp4 also involve encoding of a programming language into another.
Formally, an encoding of a language A into language B is a mapping of all terms of A into B. If there is a satisfactory encoding of A into B, B is considered at least as powerful (or at least as expressive) as A.
Properties
An informal notion of translation is not sufficient to help determine expressivity of languages, as it permits trivial encodings such as mapping all elements of A to the same element of B. Therefore, it is necessary to determine the definition of a "good enough" encoding. This notion varies with the application.
Commonly, an encoding ![[\cdot]: A \longrightarrow B](../I/m/044d9cbb92ad86be28b571a9ad37d553.png) is expected to preserve a number of properties.
is expected to preserve a number of properties.
Preservation of compositions
- soundness
- For every n-ary operator
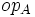 of A, there exists an n-ary operator
of A, there exists an n-ary operator 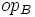 of B such that
of B such that ![\forall T_A^1,T_A^2,\dots,T_A^n, [op_A(T_A^1,T_A^2,\cdots,T_A^n)] = op_B([T_A^1],[T_A^2],\cdots,[T_A^n])](../I/m/d27072e88960357345995a63dc15fd2a.png)
- completeness
- For every n-ary operator
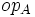 of A, there exists an n-ary operator
of A, there exists an n-ary operator 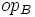 of B such that
of B such that ![\forall T_B^1,T_B^2,\dots,T_B^n, \exists T_A^1,\dots,T_A^n, op_B(T_B^1,\cdots,T_B^N) = [op_A(T_A^1,T_A^2,\cdots,T_A^n)]](../I/m/2480f3987286de046e7e67c5788ac4d6.png)
(Note: as far as the author is aware of, this criterion of completeness is never used.)
Preservation of compositions is useful insofar as it guarantees that components can be examined either separately or together without "breaking" any interesting property. In particular, in the case of compilations, this soundness guarantees the possibility of proceeding with separate compilation of components, while completeness guarantees the possibility of de-compilation.
Preservation of reductions
This assumes the existence of a notion of reduction on both language A and language B. Typically, in the case of a programming language, reduction is the relation which models the execution of a program.
We write 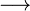 for one step of reduction and
for one step of reduction and 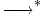 for any number of steps of reduction.
for any number of steps of reduction.
- soundness
- For every terms
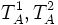 of language A, if
of language A, if 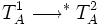 then
then ![[T_A^1] \longrightarrow^* [T_A^2]](../I/m/0d9d0e62f07dd5c49dd29e952d0e4f91.png) .
. - completeness
- For every term
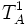 of language A and every terms
of language A and every terms 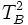 of language B, if
of language B, if ![[T_A^1] \longrightarrow^* T_B^2](../I/m/0f2a2b6ee46decb43e6f286065d5eef6.png) then there exists some
then there exists some 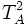 such that
such that ![T_B^2 = [T_A^2]](../I/m/80751dc7bd13ac01289c352ee9513d44.png) .
.
This preservation guarantees that both languages behave the same way. Soundness guarantees that all possible behaviours are preserved while completeness guarantees that no behaviour is added by the encoding. In particular, in the case of compilation of a programming language, soundness and completeness together mean that the compiled program behaves accordingly to the high-level semantics of the programming language.
Preservation of termination
This also assumes the existence of a notion of reduction on both language A and language B.
- soundness
- for any term
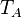 , if all reductions of
, if all reductions of 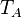 converge, then all reductions of
converge, then all reductions of ![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) converge.
converge. - completeness
- for any term
![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) , if all reductions of
, if all reductions of ![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) converge, then all reductions of
converge, then all reductions of 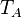 converge.
converge.
In the case of compilation of a programming language, soundness guarantees that the compilation does not introduce non-termination such as endless loops or endless recursions. The completeness property is useful when language B is used to study or test a program written in language A, possibly by extracting key parts of the code: if this study or test proves that the program terminates in B, then it also terminates in A.
Preservation of observations
This assumes the existence of a notion of observation on both language A and language B. In programming languages, typical observables are results of inputs and outputs, by opposition to pure computation. In a description language such as HTML, a typical observable is the result of page rendering.
- soundness
- for every observable
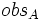 on terms of A, there exists an observable
on terms of A, there exists an observable 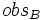 of terms of B such that for any term
of terms of B such that for any term 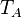 with observable
with observable 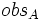 ,
, ![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) has observable
has observable 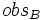 .
. - completeness
- for every observable
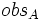 on terms of A, there exists an observable
on terms of A, there exists an observable 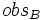 on terms of B such that for any term
on terms of B such that for any term ![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) with observable
with observable 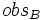 ,
, 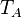 has observable
has observable 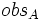 .
.
Preservation of simulations
This assumes the existence of notion of simulation on both language A and language B. In a programming languages, a program simulates another if it can perform all the same (observable) tasks and possibly some others. Simulations are used typically to describe compile-time optimizations.
- soundness
- for every terms
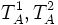 , if
, if 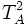 simulates
simulates 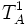 then
then ![[T_A^2]](../I/m/8ed2a44149169f28960e26b743375941.png) simulates
simulates ![[T_A^1]](../I/m/48cc1488f03cc947c0f6901abddcd841.png) .
. - completeness
- for every terms
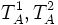 , if
, if ![[T_A^2]](../I/m/8ed2a44149169f28960e26b743375941.png) simulates
simulates ![[T_A^1]](../I/m/48cc1488f03cc947c0f6901abddcd841.png) then
then 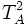 simulates
simulates 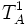 .
.
Preservation of simulations is a much stronger property than preservation of observations, which it entails. In turn, it is weaker than a property of preservation of bisimulations. As in previous cases, soundness is important for compilation, while completeness is useful for testing or proving properties.
Preservation of equivalences
This assumes the existence of a notion of equivalence on both language A and language B. Typically, this can be a notion of equality of structured data or a notion of syntactically different yet semantically identical programs, such as structural congruence or structural equivalence.
- soundness
- if two terms
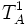 and
and 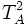 are equivalent in A, then
are equivalent in A, then ![[T_A^1]](../I/m/48cc1488f03cc947c0f6901abddcd841.png) and
and ![[T_A^2]](../I/m/8ed2a44149169f28960e26b743375941.png) are equivalent in B.
are equivalent in B. - completeness
- if two terms
![[T_A^1]](../I/m/48cc1488f03cc947c0f6901abddcd841.png) and
and ![[T_A^2]](../I/m/8ed2a44149169f28960e26b743375941.png) are equivalent in B, then
are equivalent in B, then 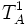 and
and 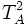 are equivalent in A.
are equivalent in A.
Preservation of distribution
This assumes the existence of a notion of distribution on both language A and language B. Typically, for compilation of distributed programs written in Acute, JoCaml or E, this means distribution of processes and data among several computers or CPUs.
- soundness
- if a term
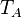 is the composition of two agents
is the composition of two agents 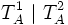 then
then ![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) must be the composition of two agents
must be the composition of two agents ![[T_A^1]~|~[T_A^2]](../I/m/9e505499b44ea3c860c82ca5f18ee078.png) .
. - completeness
- if a term
![[T_A]](../I/m/c64ef8d7f34cd88e30d1102191c3c557.png) is the composition of two agents
is the composition of two agents 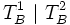 then
then  must be the composition of two agents
must be the composition of two agents 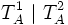 such that
such that ![[T_A^1]=T_B^1](../I/m/b1003f037271b407ba650f247aa07370.png) and
and ![[T_A^2]=T_B^2](../I/m/294925f14a3f2fde4dedf26a3f1f63ac.png) .
.