Selmer group

In arithmetic geometry, the Selmer group, named in honor of the work of Selmer (1951) by Cassels (1962), is a group constructed from an isogeny of abelian varieties. The Selmer group of an abelian variety A with respect to an isogeny f : A → B of abelian varieties can be defined in terms of Galois cohomology as

\mathrm{Sel}^{(f)}(A/K)=\bigcap_v\mathrm{ker}(H^1(G_K,\mathrm{ker}(f)))\rightarrow H^1(G_{K_v},A_v[f])/\mathrm{im}(\kappa_v))

where A_v[f] denotes the f-torsion of A_v and 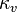$\kappa_v$ is the local Kummer map $B_v(K_v)/f(A_v(K_v))\rightarrow H^1(G_{K_v},A_v[f])$ . Note that $H^1(G_{K_v},A_v[f])/\mathrm{im}(\kappa_v)$ is isomorphic to $H^1(G_{K_v},A_v)[f]$ . Geometrically, the principal homogeneous spaces coming from elements of the Selmer group have K_v-rational points for all places v of K. The Selmer group is finite. This implies that the part of the Tate–Shafarevich group killed by f is finite due to the following exact sequence

0 → B(K)/f(A(K)) → Sel^(f)(A/K) → Ш(A/K)[f] → 0.

The Selmer group in the middle of this exact sequence is finite and effectively computable. This implies the weak Mordell–Weil theorem that its subgroup B(K)/f(A(K)) is finite. There is a notorious problem about whether this subgroup can be effectively computed: there is a procedure for computing it that will terminate with the correct answer if there is some prime p such that the p-component of the Tate–Shafarevich group is finite. It is conjectured that the Tate–Shafarevich group is in fact finite, in which case any prime p would work. However, if (as seems unlikely) the Tate–Shafarevich group has an infinite p-component for every prime p, then the procedure may never terminate.

Ralph Greenberg has generalized the notion of Selmer group to more general p-adic Galois representations and to p-adic variations of motives in the context of Iwasawa theory.

References

Cassels, John William Scott (1962), "Arithmetic on curves of genus 1. III. The Tate–Šafarevič and Selmer groups", Proceedings of the London Mathematical Society. Third Series 12: 259–296, doi:10.1112/plms/s3-12.1.259, ISSN 0024-6115, MR 0163913
Cassels, John William Scott (1991), Lectures on elliptic curves, London Mathematical Society Student Texts 24, Cambridge University Press, ISBN 978-0-521-41517-0, MR 1144763
Châtelet, François (1946), "Méthode galoisienne et courbes de genre un", Annales de L'Université de Lyon Sect. A. (3) 9: 40–49, MR 0020575
Hindry, Marc; Silverman, Joseph H. (2000), Diophantine geometry: an introduction, Graduate Texts in Mathematics 201, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98981-5
Greenberg, Ralph (1994), "Iwasawa Theory and p-adic Deformation of Motives", in Serre, Jean-Pierre; Jannsen, Uwe; Kleiman, Steven L., Motives, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-1637-0
Lang, Serge; Tate, John (1958), "Principal homogeneous spaces over abelian varieties", American Journal of Mathematics 80: 659–684, doi:10.2307/2372778, ISSN 0002-9327, MR 0106226
Selmer, Ernst S. (1951), "The Diophantine equation ax³ + by³ + cz³ = 0", Acta Mathematica 85: 203–362, doi:10.1007/BF02395746, ISSN 0001-5962, MR 0041871
Shafarevich, I. R. (1959), "The group of principal homogeneous algebraic manifolds", Doklady Akademii Nauk SSSR (in Russian) 124: 42–43, ISSN 0002-3264, MR 0106227 English translation in his collected mathematical papers
Tate, John (1958), WC-groups over p-adic fields, Séminaire Bourbaki; 10e année: 1957/1958 13, Paris: Secrétariat Mathématique, MR 0105420
Weil, André (1955), "On algebraic groups and homogeneous spaces", American Journal of Mathematics 77: 493–512, doi:10.2307/2372637, ISSN 0002-9327, MR 0074084

This article is issued from Wikipedia - version of the Thursday, February 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.