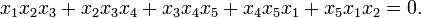Segre surface

In algebraic geometry, a Segre surface, studied by Corrado Segre (1884) and Beniamino Segre (1951), is an intersection of two quadrics in 4-dimensional projective space. They are rational surfaces isomorphic to a projective plane blown up in 5 points with no 3 on a line, and are del Pezzo surfaces of degree 4, and have 16 rational lines. The term "Segre surface" is also occasionally used for various other surfaces, such as a quadric in 3-dimensional projective space, or the hypersurface

x_1 x_2 x_3 + x_2 x_3 x_4 + x_3 x_4 x_5 + x_4 x_5 x_1 + x_5 x_1 x_2 = 0. \,

References

Segre, Corrado (1884), "Etude des différentes surfaces du 4^e ordre à conique double ou cuspidale (générale ou décomposée) considérées comme des projections de l'intersection de deux variétés quadratiques de l'espace à quatre dimensions", Mathematische Annalen (Springer Berlin / Heidelberg) 24: 313–444, doi:10.1007/BF01443412, ISSN 0025-5831
Segre, Beniamino (1951), "On the inflexional curve of an algebraic surface in S₄", The Quarterly Journal of Mathematics. Oxford. Second Series 2 (1): 216–220, doi:10.1093/qmath/2.1.216, ISSN 0033-5606, MR 0044861

This article is issued from Wikipedia - version of the Thursday, September 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.