Segal–Bargmann space
In mathematics, the Segal–Bargmann space (for Irving Segal and Valentine Bargmann), also known as the Bargmann space or Bargmann–Fock space, is the space of holomorphic functions F in n complex variables satisfying the square-integrability condition:
where here dz denotes the 2n-dimensional Lebesgue measure on Cn. It is a Hilbert space with respect to the associated inner product:
The space was introduced in the mathematical physics literature separately by Bargmann and Segal in the early 1960s; see Bargmann (1961) and Segal (1963). Basic information about the material in this section may be found in Folland (1989) and Hall (2000). Segal worked from the beginning in the infinite-dimensional setting; see Baez, Segal & Zhou (1992) and Section 10 of Hall (2000) for more information on this aspect of the subject.
Properties
A basic property of this space is that pointwise evaluation is continuous, meaning that for each a in Cn, there is a constant C such that
It then follows from the Riesz representation theorem that there exists a unique Fa in the Segal–Bargmann space such that
The function Fa may be computed explicitly as
where, explicitly,
The function Fa is called the coherent state with parameter a, and the function
is known as the reproducing kernel for the Segal–Bargmann space. Note that
meaning that integration against the reproducing kernel simply gives back (i.e., reproduces) the function F, provided, of course that F is holomorphic!
Note that
It follows from the Cauchy–Schwarz inequality that elements of the Segal–Bargmann space satisfy the pointwise bounds
Quantum mechanical interpretation
One may interpret a unit vector in the Segal–Bargmann space as the wave function for a quantum particle moving in Rn. In this view, Cn plays the role of the classical phase space, whereas Rn is the configuration space. The restriction that F be holomorphic is essential to this interpretation; if F were an arbitrary square-integrable function, it could be localized into an arbitrarily small region of the phase space, which would go against the uncertainty principle. Since, however, F is required to be holomorphic, it satisfies the pointwise bounds described above, which provides a limit on how concentrated F can be in any region of phase space.
Given a unit vector F in the Segal–Bargmann space, the quantity
may be interpreted as a sort of phase space probability density for the particle. Since the above quantity is manifestly non-negative, it cannot coincide with the Wigner function of the particle, which usually has some negative values. In fact, the above density coincides with the Husimi function of the particle, which is obtained from the Wigner function by smearing with a Gaussian. This connection will be made more precise below, after we introduce the Segal–Bargmann transform.
The canonical commutation relations
One may introduce annihilation operators aj and creation operators aj* on the Segal–Bargann space by setting
and
These operators satisfy the same relations as the usual creation and annihilation operators, namely, the aj's and aj*'s commute among themselves and
Furthermore, the adjoint of aj with respect to the inner product in (x) is aj*. (This is suggested by the notation, but not at all obvious from the formulas for aj and aj*!) Indeed, Bargmann was led to introduce the particular form of the inner product on the Segal–Bargmann space precisely so that the creation and annihilation operators would be adjoints of each other.
We may now construct self-adjoint "position" and "momentum" operators Aj and Bj by the formulas:
These operators satisfy the ordinary canonical commutation relations. It can be shown that Aj and Bj satisfy the exponentiated commutation relations (i.e., the Weyl relations) and that they act irreducibly on the Segal–Bargmann space; see Section 14.4 of Hall (2013).
The Segal–Bargmann transform
Since the operators Aj and Bj from the previous section satisfy the Weyl relations and act irreducibly on the Segal–Bargmann space, the Stone–von Neumann theorem applies. Thus, there is a unitary map B from the position Hilbert space L2(ℝn) to the Segal–Bargmann space that intertwines these operators with the usual position and momentum operators.
The map B may be computed explicitly as a modified double Weierstrass transform,
where dx is the n-dimensional Lebesgue measure on ℝn and where z is in ℂn. See Bargmann (1961) and Section 14.4 of Hall (2013). One can also describe (Bf)(z) as the inner product of f with an appropriately normalized coherent state with parameter z, where, now, we express the coherent states in the position representation instead of in the Segal–Bargmann space.
We may now be more precise about the connection between the Segal–Bargmann space and the Husimi function of a particle. If f is a unit vector in L ² (ℝn), then we may form a probability density on ℂn as
The claim is then that the above density is the Husimi function of f, which may be obtained from the Wigner function of f by convolving with a double Gaussian (the Weierstrass transform). This fact is easily verified by using the formula for Bf along with the standard formula for the Husimi function in terms of coherent states.
Since B is unitary, its Hermitian adjoint is its inverse. We thus obtain one inversion formula for B as
Since, however, Bf is a holomorphic function, there can be many integrals involving Bf that give the same value. (Think of the Cauchy integral formula.) Thus, there can be many different inversion formulas for the Segal–Bargmann transform B.
Another useful inversion formula is[1]
where  . This inversion formula may be understood as saying that the position "wave function" f may be obtained from the phase-space "wave function" Bf by integrating out the momentum variables. This is to be contrasted to the Wigner function, where the position probability density is obtained from the phase space (quasi-)probability density by integrating out the momentum variables.
. This inversion formula may be understood as saying that the position "wave function" f may be obtained from the phase-space "wave function" Bf by integrating out the momentum variables. This is to be contrasted to the Wigner function, where the position probability density is obtained from the phase space (quasi-)probability density by integrating out the momentum variables.
Generalizations
There are various generalizations of the Segal–Bargmann transform. In one of these,[2][3] the role of the configuration space Rn is played by the group manifold of a compact Lie group, such as SU(N). The role of the phase space Cn is then played by the complexification of the compact Lie group, such as SL(N;C) in the case of SU(N). The various Gaussians appearing in the ordinary Segal–Bargmann space and transform are replaced by heat kernels. See Olafsson (2014) for more information.
See also
References
- ↑ B.C. Hall, "The range of the heat operator", in The Ubiquitous Heat Kernel, edited by Jay Jorgensen and Lynne H. Walling, AMS 2006, pp. 203–231
- ↑ B.C. Hall, "The Segal–Bargmann 'coherent state' transform for compact Lie groups", J. Functional Analysis 122 (1994), 103–151
- ↑ B.C. Hall, "The inverse Segal–Bargmann transform for compact Lie groups", J. Functional Analysis 143 (1997), 98–116
Sources
- Bargmann, V. (1961), "On a Hilbert space of analytic functions and an associated integral transform", Communications on Pure and Applied Mathematics 14 (3): 187, doi:10.1002/cpa.3160140303
- Segal, I. E. (1963), "Mathematical problems of relativistic physics", in Kac, M., Proceedings of the Summer Seminar, Boulder, Colorado, 1960, Vol. II, Lectures in Applied Mathematics, American Mathematical Society, Chap. VI
- Folland, G. (1989), Harmonic Analysis in Phase Space, Princeton University Press
- Baez, J.; Segal, I. E.; Zhou, Z. (1992), Introduction to Algebraic and Constructive Quantum Field Theory, Princeton University Press
- Hall, B. C. (2000), "Holomorphic methods in analysis and mathematical physics", in First Summer School in Analysis and Mathematical Physics (S. Pérez-Esteva and C. Villegas-Blas, Eds.), 1–59, Contemporary Mathematics 260, Amer. Math. Soc.
- Hall, B. C. (2013), Quantum Theory for Mathematicians, Springer
- Olafsson, G. (2014), The Segal–Bargmann Transform on Euclidean Space and Generalizations, World Scientific



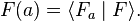



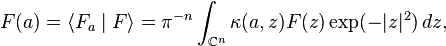



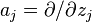

![[a_j,a_k^*] = \delta_{j,k}](../I/m/201a7b63dfc1ec66d8d91bd65077b6d5.png)


![(Bf)(z) = \int_{\Bbb R^n} \exp[-(z \cdot z - 2 \sqrt{2} z \cdot x + x \cdot x)/2]f(x) \, dx ~,](../I/m/c6ca8949b916ee0a051310f2fab02f0d.png)

(z) \, dz ~.](../I/m/976998d8fc0aeef7cba2a28c5119a6ea.png)
