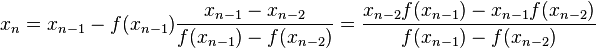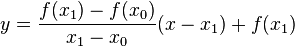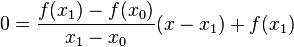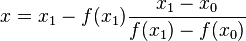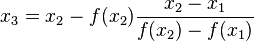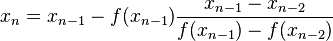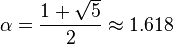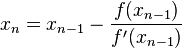Secant method
In numerical analysis, the secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function f. The secant method can be thought of as a finite difference approximation of Newton's method. However, the method was developed independently of Newton's method, and predates it by over 3,000 years.[1]
The method
The secant method is defined by the recurrence relation
As can be seen from the recurrence relation, the secant method requires two initial values, x0 and x1, which should ideally be chosen to lie close to the root.
Derivation of the method
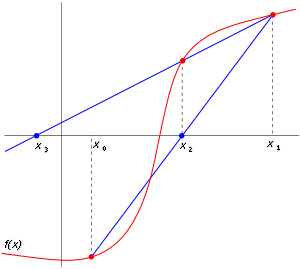
Starting with initial values x0 and x1, we construct a line through the points (x0, f(x0)) and (x1, f(x1)), as demonstrated in the picture on the right. In point-slope form, this line has the equation
We find the root of this line – the value of x such that y = 0 – by solving the following equation for x:
The solution is
We then use this new value of x as x2 and repeat the process using x1 and x2 instead of x0 and x1. We continue this process, solving for x3, x4, etc., until we reach a sufficiently high level of precision (a sufficiently small difference between xn and xn - 1).
- …
Convergence
The iterates 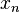 of the secant method converge to a root of
of the secant method converge to a root of  , if the initial values
, if the initial values 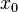 and
and 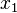 are sufficiently close to the root. The order of convergence is α, where
are sufficiently close to the root. The order of convergence is α, where
is the golden ratio. In particular, the convergence is superlinear, but not quite quadratic.
This result only holds under some technical conditions, namely that  be twice continuously differentiable and the root in question be simple (i.e., with multiplicity 1).
be twice continuously differentiable and the root in question be simple (i.e., with multiplicity 1).
If the initial values are not close enough to the root, then there is no guarantee that the secant method converges. There is no general definition of "close enough", but the criterion has to do with how "wiggly" the function is on the interval ![[~x_0,~x_1~]](../I/m/831b01fe229d3bdbc6f122bf85357cc3.png) . For example, if
. For example, if  is differentiable on that interval and there is a point where
is differentiable on that interval and there is a point where 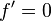 on the interval, then the algorithm may not converge.
on the interval, then the algorithm may not converge.
Comparison with other root-finding methods
The secant method does not require that the root remain bracketed like the bisection method does, and hence it does not always converge. The false position method (or regula falsi) uses the same formula as the secant method. However, it does not apply the formula on  and
and 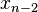 , like the secant method, but on
, like the secant method, but on  and on the last iterate
and on the last iterate 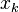 such that
such that 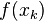 and
and 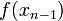 have a different sign. This means that the false position method always converges.
have a different sign. This means that the false position method always converges.
The recurrence formula of the secant method can be derived from the formula for Newton's method
by using the finite difference approximation
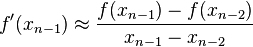 .
.
The secant method can be interpreted as a method in which the derivative is replaced by an approximation and is thus a Quasi-Newton method.
If we compare Newton's method with the secant method, we see that Newton's method converges faster (order 2 against α ≈ 1.6). However, Newton's method requires the evaluation of both  and its derivative
and its derivative 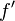 at every step, while the secant method only requires the evaluation of
at every step, while the secant method only requires the evaluation of  . Therefore, the secant method may occasionally be faster in practice. For instance, if we assume that evaluating
. Therefore, the secant method may occasionally be faster in practice. For instance, if we assume that evaluating  takes as much time as evaluating its derivative and we neglect all other costs, we can do two steps of the secant method (decreasing the logarithm of the error by a factor α² ≈ 2.6) for the same cost as one step of Newton's method (decreasing the logarithm of the error by a factor 2), so the secant method is faster. If however we consider parallel processing for the evaluation of the derivative, Newton's method proves its worth, being faster in time, though still spending more steps.
takes as much time as evaluating its derivative and we neglect all other costs, we can do two steps of the secant method (decreasing the logarithm of the error by a factor α² ≈ 2.6) for the same cost as one step of Newton's method (decreasing the logarithm of the error by a factor 2), so the secant method is faster. If however we consider parallel processing for the evaluation of the derivative, Newton's method proves its worth, being faster in time, though still spending more steps.
Generalizations
Broyden's method is a generalization of the secant method to more than one dimension.
The following graph shows the function f in red and the last secant line in bold blue. In the graph, the x-intercept of the secant line seems to be a good approximation of the root of f.

A computational example
The Secant method is applied to find a root of the function f(x) = x2 − 612. Here is an implementation in the Matlab language (from calculation, we expect that the iteration converges at x = 24.7386):
f=@(x) x^2 - 612;
x(1)=10;
x(2)=30;
for i=3:7
x(i) = x(i-1) - (f(x(i-1)))*((x(i-1) - x(i-2))/(f(x(i-1)) - f(x(i-2))));
end
root=x(7)
Notes
- ↑ Papakonstantinou, J., The Historical Development of the Secant Method in 1-D, retrieved 2011-06-29
See also
References
- Kaw, Autar; Kalu, Egwu (2008), Numerical Methods with Applications (1st ed.).
- Allen, Myron B.; Isaacson, Eli L. (1998). Numerical analysis for applied science. John Wiley & Sons. pp. 188–195. ISBN 978-0-471-55266-6.
External links
- Secant Method Notes, PPT, Mathcad, Maple, Mathematica, Matlab at Holistic Numerical Methods Institute
- Weisstein, Eric W., "Secant Method", MathWorld.
| ||||||||||||||||||||||