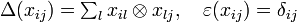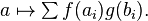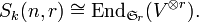Schur algebra
In mathematics, Schur algebras, named after Issai Schur, are certain finite-dimensional algebras closely associated with Schur–Weyl duality between general linear and symmetric groups. They are used to relate the representation theories of those two groups. Their use was promoted by the influential monograph of J. A. Green first published in 1980.[1] The name "Schur algebra" is due to Green. In the modular case (over infinite fields of positive characteristic) Schur algebras were used by Gordon James and Karin Erdmann to show that the (still open) problems of computing decomposition numbers for general linear groups and symmetric groups are actually equivalent.[2] Schur algebras were used by Friedlander and Suslin to prove finite generation of cohomology of finite group schemes.[3]
Construction
The Schur algebra 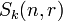 can be defined for any commutative ring
can be defined for any commutative ring  and integers
and integers 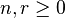 . Consider the algebra
. Consider the algebra ![k[x_{ij}]](../I/m/ab952b433447607db11d502fb989adf8.png) of polynomials (with coefficients in
of polynomials (with coefficients in  ) in
) in  commuting variables
commuting variables 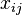 , 1 ≤ i, j ≤
, 1 ≤ i, j ≤  . Denote by
. Denote by 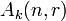 the homogeneous polynomials of degree
the homogeneous polynomials of degree  . Elements of
. Elements of 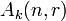 are k-linear combinations of monomials formed by multiplying together
are k-linear combinations of monomials formed by multiplying together  of the generators
of the generators 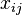 (allowing repetition). Thus
(allowing repetition). Thus
Now, ![k[x_{ij}]](../I/m/ab952b433447607db11d502fb989adf8.png) has a natural coalgebra structure with comultiplication
has a natural coalgebra structure with comultiplication  and counit
and counit  the algebra homomorphisms given on generators by
the algebra homomorphisms given on generators by
Since comultiplication is an algebra homomorphism, ![k[x_{ij}]](../I/m/ab952b433447607db11d502fb989adf8.png) is a bialgebra. One easily
checks that
is a bialgebra. One easily
checks that 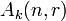 is a subcoalgebra of the bialgebra
is a subcoalgebra of the bialgebra ![k[x_{ij}]](../I/m/ab952b433447607db11d502fb989adf8.png) , for every r ≥ 0.
, for every r ≥ 0.
Definition. The Schur algebra (in degree  ) is the algebra
) is the algebra  . That is,
. That is, 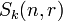 is the linear dual of
is the linear dual of 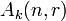 .
.
It is a general fact that the linear dual of a coalgebra  is an algebra in a natural way, where the multiplication in the algebra is induced by dualizing the comultiplication in the coalgebra. To see this, let
is an algebra in a natural way, where the multiplication in the algebra is induced by dualizing the comultiplication in the coalgebra. To see this, let
and, given linear functionals  ,
,  on
on  , define their product to be the linear functional given by
, define their product to be the linear functional given by
The identity element for this multiplication of functionals is the counit in  .
.
Main properties
- One of the most basic properties expresses
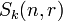 as a centralizer algebra. Let
as a centralizer algebra. Let  be the space of rank
be the space of rank  column vectors over
column vectors over  , and form the tensor power
, and form the tensor power
Then the symmetric group 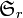 on
on  letters acts naturally on the tensor space by place permutation, and one has an isomorphism
letters acts naturally on the tensor space by place permutation, and one has an isomorphism
In other words, 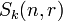 may be viewed as the algebra of endomorphisms of tensor space commuting with the action of the symmetric group.
may be viewed as the algebra of endomorphisms of tensor space commuting with the action of the symmetric group.
-
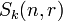 is free over
is free over  of rank given by the binomial coefficient
of rank given by the binomial coefficient  .
.
- Various bases of
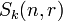 are known, many of which are indexed by pairs of semistandard Young tableaux of shape
are known, many of which are indexed by pairs of semistandard Young tableaux of shape  , as
, as  varies over the set of partitions of
varies over the set of partitions of  into no more than
into no more than  parts.
parts.
- In case k is an infinite field,
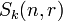 may also be identified with the enveloping algebra (in the sense of H. Weyl) for the action of the general linear group
may also be identified with the enveloping algebra (in the sense of H. Weyl) for the action of the general linear group 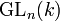 acting on tensor space (via the diagonal action on tensors, induced from the natural action of
acting on tensor space (via the diagonal action on tensors, induced from the natural action of 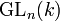 on
on  given by matrix multiplication).
given by matrix multiplication).
- Schur algebras are "defined over the integers". This means that they satisfy the following change of scalars property:
-
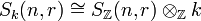
- for any commutative ring
 .
.
- Schur algebras provide natural examples of quasihereditary algebras[4] (as defined by Cline, Parshall, and Scott), and thus have nice homological properties. In particular, Schur algebras have finite global dimension.
Generalizations
- Generalized Schur algebras (associated to any reductive algebraic group) were introduced by Donkin in the 1980s.[5] These are also quasihereditary.
- Around the same time, Dipper and James[6] introduced the quantized Schur algebras (or q-Schur algebras for short), which are a type of q-deformation of the classical Schur algebras described above, in which the symmetric group is replaced by the corresponding Hecke algebra and the general linear group by an appropriate quantum group.
- There are also generalized q-Schur algebras, which are obtained by generalizing the work of Dipper and James in the same way that Donkin generalized the classical Schur algebras.[7]
- There are further generalizations, such as the affine q-Schur algebras[8] related to affine Kac–Moody Lie algebras and other generalizations, such as the cyclotomic q-Schur algebras[9] related to Ariki-Koike algebras (which are q-deformations of certain complex reflection groups).
The study of these various classes of generalizations forms an active area of contemporary research.
References
- ↑ J. A. Green, Polynomial Representations of GLn, Springer Lecture Notes 830, Springer-Verlag 1980. MR 2349209, ISBN 978-3-540-46944-5, ISBN 3-540-46944-3
- ↑ Karin Erdmann, Decomposition numbers for symmetric groups and composition factors of Weyl modules. Journal of Algebra 180 (1996), 316–320. doi:10.1006/jabr.1996.0067 MR 1375581
- ↑ Eric Friedlander and Andrei Suslin, Cohomology of finite group schemes over a field. Inventiones Mathematicae 127 (1997), 209--270. MR 1427618 doi:10.1007/s002220050119
- ↑ Edward Cline, Brian Parshall, and Leonard Scott, Finite-dimensional algebras and highest weight categories. Journal für die Reine und Angewandte Mathematik [Crelle's Journal] 391 (1988), 85–99. MR 0961165
- ↑ Stephen Donkin, On Schur algebras and related algebras, I. Journal of Algebra 104 (1986), 310–328. doi:10.1016/0021-8693(86)90218-8 MR 0866778
- ↑ Richard Dipper and Gordon James, The q-Schur algebra. Proceedings of the London Math. Society (3) 59 (1989), 23–50. doi:10.1112/plms/s3-59.1.23 MR 0997250
- ↑ Stephen Doty, Presenting generalized q-Schur algebras. Representation Theory 7 (2003), 196--213 (electronic). doi:10.1090/S1088-4165-03-00176-6
- ↑ R. M. Green, The affine q-Schur algebra. Journal of Algebra 215 (1999), 379--411. doi:10.1006/jabr.1998.7753
- ↑ Richard Dipper, Gordon James, and Andrew Mathas, Cyclotomic q-Schur algebras. Math. Zeitschrift 229 (1998), 385--416. doi:10.1007/PL00004665 MR 1658581
Further reading
- Stuart Martin, Schur Algebras and Representation Theory, Cambridge University Press 1993. MR 2482481, ISBN 978-0-521-10046-5
- Andrew Mathas, Iwahori-Hecke algebras and Schur algebras of the symmetric group, University Lecture Series, vol.15, American Mathematical Society, 1999. MR 1711316, ISBN 0-8218-1926-7
- Hermann Weyl, The Classical Groups. Their Invariants and Representations. Princeton University Press, Princeton, N.J., 1939. MR 0000255, ISBN 0-691-05756-7
![k[x_{ij}] = \bigoplus_{r\ge 0} A_k(n, r).](../I/m/37b66bdf56e45b9c768506b72302a464.png)