Schur-convex function
In mathematics, a Schur-convex function, also known as S-convex, isotonic function and order-preserving function is a function 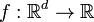 that for all
that for all 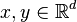 such that
such that  is majorized by
is majorized by 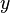 , one has that
, one has that  . Named after Issai Schur, Schur-convex functions are used in the study of majorization. Every function that is convex and symmetric is also Schur-convex. The opposite implication is not true, but all Schur-convex functions are symmetric (under permutations of the arguments).[1]
. Named after Issai Schur, Schur-convex functions are used in the study of majorization. Every function that is convex and symmetric is also Schur-convex. The opposite implication is not true, but all Schur-convex functions are symmetric (under permutations of the arguments).[1]
Schur-concave function
A function f is 'Schur-concave' if its negative, -f, is Schur-convex.
Schur-Ostrowski criterion
If f is symmetric and all first partial derivatives exist, then f is Schur-convex if and only if
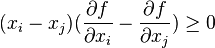 for all
for all 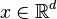
holds for all 1≤i≠j≤d.[2]
Examples
-
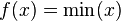 is Schur-concave while
is Schur-concave while 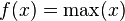 is Schur-convex. This can be seen directly from the definition.
is Schur-convex. This can be seen directly from the definition.
- The Shannon entropy function
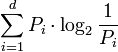 is Schur-concave.
is Schur-concave.
- The Rényi entropy function is also Schur-concave.
-
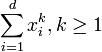 is Schur-convex.
is Schur-convex.
- The function
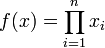 is Schur-concave, when we assume all
is Schur-concave, when we assume all 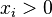 . In the same way, all the Elementary symmetric functions are Schur-concave, when
. In the same way, all the Elementary symmetric functions are Schur-concave, when 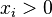 .
.
- A natural interpretation of majorization is that if
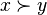 then
then  is more spread out than
is more spread out than 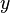 . So it is natural to ask if statistical measures of variability are Schur-convex. The variance and standard deviation are Schur-convex functions, while the Median absolute deviation is not.
. So it is natural to ask if statistical measures of variability are Schur-convex. The variance and standard deviation are Schur-convex functions, while the Median absolute deviation is not.
- If
 is a convex function defined on a real interval, then
is a convex function defined on a real interval, then 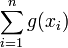 is Schur-convex.
is Schur-convex.
- A probability example: If
 are exchangeable random variables, then the function
are exchangeable random variables, then the function 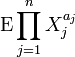 is Schur-convex as a function of
is Schur-convex as a function of 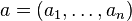 , assuming that the expectations exist.
, assuming that the expectations exist.
- The Gini coefficient is strictly Schur concave.
References
See also
This article is issued from Wikipedia - version of the Saturday, January 23, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.