Schilder's theorem
In mathematics, Schilder's theorem is a result in the large deviations theory of stochastic processes. Roughly speaking, Schilder's theorem gives an estimate for the probability that a (scaled-down) sample path of Brownian motion will stray far from the mean path (which is constant with value 0). This statement is made precise using rate functions. Schilder's theorem is generalized by the Freidlin–Wentzell theorem for Itō diffusions.
Statement of the theorem
Let B be a standard Brownian motion in d-dimensional Euclidean space Rd starting at the origin, 0 ∈ Rd; let W denote the law of B, i.e. classical Wiener measure. For ε > 0, let Wε denote the law of the rescaled process (√ε)B. Then, on the Banach space C0 = C0([0, T]; Rd) of continuous functions ![f : [0,T] \longrightarrow \mathbf{R}^d](../I/m/395fb4a02195cea4982191e91f9ae7cd.png) such that
such that 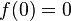 , equipped with the supremum norm ||·||∞, the probability measures Wε satisfy the large deviations principle with good rate function I : C0 → R ∪ {+∞} given by
, equipped with the supremum norm ||·||∞, the probability measures Wε satisfy the large deviations principle with good rate function I : C0 → R ∪ {+∞} given by
if ω is absolutely continuous, and I(ω) = +∞ otherwise. In other words, for every open set G ⊆ C0 and every closed set F ⊆ C0,
and
Example
Taking ε = 1 ⁄ c2, one can use Schilder's theorem to obtain estimates for the probability that a standard Brownian motion B strays further than c from its starting point over the time interval [0, T], i.e. the probability
as c tends to infinity. Here Bc(0; ||·||∞) denotes the open ball of radius c about the zero function in C0, taken with respect to the supremum norm. First note that
Since the rate function is continuous on A, Schilder's theorem yields
making use of the fact that the infimum over paths in the collection A is attained for ω(t) = t ⁄ T. This result can be heuristically interpreted as saying that, for large c and/or large T
or, in other words,
In fact, the above probability can be estimated more precisely as follows: for B a standard Brownian motion in Rn, and any T, c and ε > 0, it holds that
References
- Dembo, Amir; Zeitouni, Ofer (1998). Large deviations techniques and applications. Applications of Mathematics (New York) 38 (Second ed.). New York: Springer-Verlag. pp. xvi+396. ISBN 0-387-98406-2. MR 1619036. (See theorem 5.2)
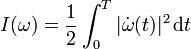
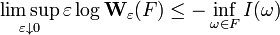
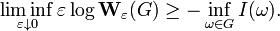
![\mathbf{W} (C_{0} \setminus \mathbf{B}_{c} (0; \| \cdot \|_{\infty})) \equiv \mathbf{P} \big[ \| B \|_{\infty} > c \big],](../I/m/5cbce0671f85807016822c178c809b69.png)
![\| B \|_{\infty} > c \iff \sqrt{\varepsilon} B \in A := \big\{ \omega \in C_{0} \big| | \omega(t) | > 1 \mbox{ for some } t \in [0, T] \big\}.](../I/m/483afbea83fbdc52ab61b50be05ad692.png)
![\lim_{c \to \infty} \frac{1}{c^{2}} \log \mathbf{P} \big[ \| B \|_{\infty} > c \big]](../I/m/5c492a2421914e4be31feb9dc88707a3.png)
![= \lim_{\varepsilon \to 0} \epsilon \log \mathbf{P} \big[ \sqrt{\varepsilon} B \in A \big]](../I/m/5966cbb6a5741ec5726e3d2b25eb4424.png)
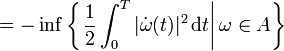
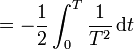
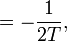
![\frac{1}{c^{2}} \log \mathbf{P} \big[ \| B \|_{\infty} > c \big] \approx - \frac{1}{2 T},](../I/m/8b8c70e519e55b58ea0185351cfde5b3.png)
![\mathbf{P} \big[ \| B \|_{\infty} > c \big] \approx \exp \left( - \frac{c^{2}}{2 T} \right).](../I/m/e9d01255188af1313e654ac20cbc02c1.png)
![\mathbf{P} \left[ \sup_{0 \leq t \leq T} \big| \sqrt{\varepsilon} B_{t} \big| \geq c \right] \leq 4 n \exp \left( - \frac{c^{2}}{2 n T \varepsilon} \right).](../I/m/861b938d95ca4dd4e628fa3a9afd22ab.png)