Scheffé’s lemma

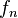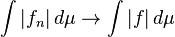In mathematics, Scheffé's lemma is a proposition in measure theory concerning the convergence of sequences of integrals. It states that, if $f_n$ is a sequence of integrable functions on a measure space $(X,\Sigma,\mu)$ that converges almost everywhere to another integrable function $f$ , then $\int |f_n - f| \, d\mu \to 0$ if and only if $\int | f_n | \, d\mu \to \int | f | \, d\mu$ .^[1]

Applications

Applied to probability theory, Scheffe's theorem, in the form stated here, implies that almost everywhere pointwise convergence of the probability density functions of a sequence of $\mu$ -absolutely continuous random variables implies convergence in distribution of those random variables.

History

Henry Scheffé published a proof of the statement on convergence of probability densities in 1947. The result however is a special case of a theorem by Frigyes Riesz about convergence in L^p spaces published in 1928.^[2]

References

↑ David Williams (1991). Probability with Martingales. New York: Cambridge University Press. p. 55.
↑ Norbert Kusolitsch (September 2010). "Why the theorem of Scheffé should be rather called a theorem of Riesz". Periodica Mathematica Hungarica 61 (1-2): 225–229. doi:10.1007/s10998-010-3225-6.

This article is issued from Wikipedia - version of the Friday, August 07, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.