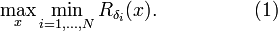Scenario optimization

The scenario approach or scenario optimization approach is a technique for obtaining solutions to robust optimization and chance-constrained optimization problems based on randomization of the constraints. The technique has existed for decades as a heuristic approach and has more recently been given a systematic theoretical foundation.

Description

In optimization, robustness features translate into constraints that are parameterized in the uncertain elements of the problem. The scenario method[1][2][3] simply consists in extracting at random some instances of the uncertainty, and then finding the optimal solution of a problem where only the constraints associated to the extracted uncertainty instances are considered. The theory tells the user how “robust” this solution is, that is whether and to what extent the found solution satisfies the constraints occurring for other unseen instances of the uncertainty. Thus, this theory justifies at a solid theoretical level the use of randomization in robust and chance-constrained optimization.


When the constraints are convex (e.g. in semidefinite problems involving LMIs, Linear Matrix Inequalities), the theoretical results are tight. This means that the number N of constraints that need be sampled as prescribed by the theory is provably the smallest possible number to achieve the desired robustness level. Extensions to more complex, non-convex, set-ups is still object of investigation.

Along the scenario approach, it is also possible to pursue a risk-return trade-off,.[4][5][6] Paper [7] provides a full-fledged method to apply this approach to control. First N constraints are sampled and then the user starts removing some of them in succession. This can be done in different ways, even according to greedy algorithms. After elimination of one more constraint, the optimal solution is updated, and the corresponding optimal value is determined. As this procedure moves on, the user constructs on-the-go the “curve of values”, i.e. the curve representing the value achieved after removing of an increasing number of constraints, while the scenario theory provides precise evaluations of how robust the various solutions are. The final outcome is a risk (robustness) vs. return (optimization value) graph as depicted in Figure 1, from which the user can choose his favorite risk-return compromise.

Example

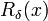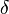R_\delta(x) represents the return of an investment; it depends on our vector of investment choices x and on the market state \delta which will be experienced at the end of the investment period.

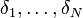Given a stochastic model for the possible market conditions, we consider N of the possible states \delta_1, \dots, \delta_N (randomization of uncertainty). Alternatively, the scenarios \delta_i can be obtained from a record of past observations, in which case we can see them as being “sampled by nature”.

We solve the scenario optimization program

\max_x \min_{i=1,\dots,N} R_{\delta_i}(x). \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)

That is, we choose a portfolio vector x so as to give the best possible return in the worst-case scenario of those considered.[8][9]

After solving (1) we obtain an optimal investment strategy 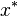x^\ast and the corresponding optimal return 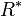R^\ast for the worst-case scenario of those considered. The 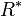R^\ast value has been obtained by looking at N possible market states only and therefore it is guaranteed to be achieved if one of these market states occurs. Further, scenario theory tells us that the solution is robust up to a level \epsilon: that is, the return 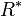R^\ast will be achieved with probability 1 - \epsilon unconditional on the market state.

Application fields

Prediction, systems theory, regression, control, financial mathematics, machine learning, decision making, supply chain, management.

References

  1. ↑ G. Calafiore and M.C. Campi. Uncertain Convex Programs: Randomized Solutions and Confidence Levels. Mathematical Programming, 102: 25–46, 2005.
  2. ↑ G. Calafiore and M.C. Campi. "The scenario approach to robust control design," IEEE Transactions on Automatic Control, 51(5). 742-753, 2006.
  3. ↑ M.C. Campi and S. Garatti. The Exact Feasibility of Randomized Solutions of Uncertain Convex Programs. SIAM J. on Optimization, 19, no.3: 1211–1230, 2008.
  4. ↑ M.C. Campi and S. Garatti. Chance-constrained optimization via randomization: feasibility and optimality. Optimization Online, 2008.
  5. ↑ G.C. Calafiore. Random Convex Programs. SIAM J. on Optimization, 20(6) 3427-3464, 2010.
  6. ↑ M.C. Campi and S. Garatti. A Sampling-and-Discarding Approach to Chance-Constrained Optimization: Feasibility and Optimality. Journal of Optimization Theory and Applications, 148, Number 2, 257–280, 2011.
  7. ↑ S. Garatti and M.C. Campi. Modulating Robustness in Control Design: Principles and Algorithms.. IEEE Control Systems Magazine, 33, 36–51, 2013.
  8. ↑ B.K. Pagnoncelli, D. Reich and M.C. Campi. Risk-Return Trade-off with the Scenario Approach in Practice: A Case Study in Portfolio Selection. J. of Optimization Theory and Applications, 155: 707-722, 2012.
  9. ↑ G.C. Calafiore. Direct data-driven portfolio optimization with guaranteed shortfall probability. Automatica, 49(2) 370-380, 2013.
This article is issued from Wikipedia - version of the Saturday, October 03, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.