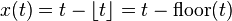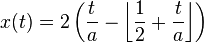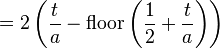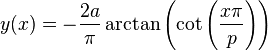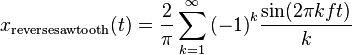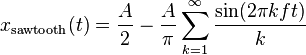Sawtooth wave

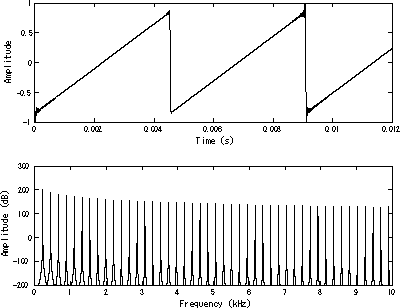
A bandlimited sawtooth wave pictured in the time domain (top) and frequency domain (bottom). The fundamental is at 220 Hz (A3).

The sawtooth wave (or saw wave) is a kind of non-sinusoidal waveform. It is so named based on its resemblance to the teeth of a saw.

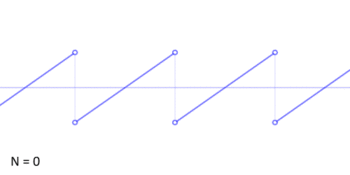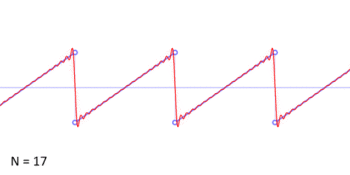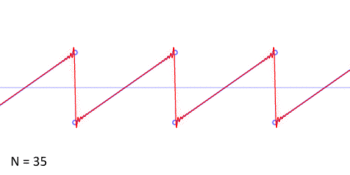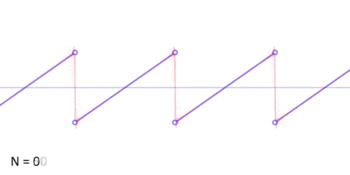
The convention is that a sawtooth wave ramps upward and then sharply drops. However, in a "reverse (or inverse) sawtooth wave", the wave ramps downward and then sharply rises. It can also be considered the extreme case of an asymmetric triangle wave.[1]

The piecewise linear function

x(t) = t - \lfloor t \rfloor = t - \operatorname{floor}(t)

based on the floor function of time t is an example of a sawtooth wave with period 1.

A more general form, in the range −1 to 1, and with period a, is

x(t) = 2 \left( {t \over a} - \left\lfloor {1 \over 2} + {t \over a}\right\rfloor \right)
= 2 \left( {t \over a} - \operatorname{floor} \left( {1 \over 2} + {t \over a} \right) \right)

This sawtooth function has the same phase as the sine function.

Another function in trigonometric terms with period p and amplitude a:

y(x) = -\frac{2a}{\pi}\arctan \left( \cot \left(\frac{x \pi}{p} \right) \right)

While a square wave is constructed from only odd harmonics, a sawtooth wave's sound is harsh and clear and its spectrum contains both even and odd harmonics of the fundamental frequency. Because it contains all the integer harmonics, it is one of the best waveforms to use for subtractive synthesis of musical sounds, particularly bowed string instruments like violins and cellos, since the slip-stick behavior of the bow drives the strings with a sawtooth-like motion.[2]
Additive Sawtooth Demo
220Hz Sawtooth wave created by harmonics added every second over sine wave.
Problems playing this file? See media help.

A sawtooth can be constructed using additive synthesis. The infinite Fourier series

x_\mathrm{reversesawtooth}(t) = \frac {2}{\pi}\sum_{k=1}^{\infty} {(-1)}^{k} \frac {\sin (2\pi kft)}{k}

converges to a reverse (inverse) sawtooth wave. A conventional sawtooth can be constructed using

x_\mathrm{sawtooth}(t) = \frac{A}{2}-\frac {A}{\pi}\sum_{k=1}^{\infty}\frac {\sin (2\pi kft)}{k}

Where A is amplitude.

In digital synthesis, these series are only summed over k such that the highest harmonic, Nmax, is less than the Nyquist frequency (half the sampling frequency). This summation can generally be more efficiently calculated with a fast Fourier transform. If the waveform is digitally created directly in the time domain using a non-bandlimited form, such as y = x - floor(x), infinite harmonics are sampled and the resulting tone contains aliasing distortion.

Animation of the additive synthesis of a sawtooth wave with an increasing number of harmonics

An audio demonstration of a sawtooth played at 440 Hz (A4) and 880 Hz (A5) and 1760 Hz (A6) is available below. Both bandlimited (non-aliased) and aliased tones are presented.
Sawtooth aliasing demo
Sawtooth waves played bandlimited and aliased at 440 Hz, 880 Hz, and 1760 Hz
Problems playing this file? See media help.

Applications

See also

Sine, square, triangle, and sawtooth waveforms

References

  1. ↑ "Fourier Series-Triangle Wave - from Wolfram MathWorld". Mathworld.wolfram.com. 2012-07-02. Retrieved 2012-07-11.
  2. ↑ http://homepages.abdn.ac.uk/mth192/pages/html/music.pdf page 42

External links

This article is issued from Wikipedia - version of the Friday, February 12, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.