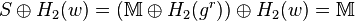Sakai–Kasahara scheme
The Sakai–Kasahara scheme, also known as the Sakai–Kasahara key encryption algorithm (SAKKE), is an identity-based encryption (IBE) system proposed by Ryuichi Sakai and Masao Kasahara in 2003.[1] Alongside the Boneh–Franklin scheme, this is one of a small number of commercially implemented identity-based encryption schemes. It is an application of pairings over elliptic curves and finite fields. A security proof for the algorithm was produced in 2005 by Chen and Cheng.[2] SAKKE is described in Internet Engineering Task Force (IETF) RFC 6508.[3]
As a specific method for identity-based encryption, the primary use case is to allow anyone to encrypt a message to a user when the sender only knows the public identity (e.g. email address) of the user. In this way, this scheme removes the requirement for users to share public certificates for the purpose of encryption.
Description of Scheme
The Sakai–Kasahara scheme allows the encryption of a message 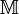 to an receiver with a specific identity,
to an receiver with a specific identity,  . Only the entity with the private key,
. Only the entity with the private key, 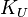 , associated to the identity,
, associated to the identity,  , will be capable of decrypting the message.
, will be capable of decrypting the message.
As part of the scheme, both the sender and receiver must trust a Private Key Generator (PKG), also known as a Key Management Server (KMS). The purpose of the PKG is to create the receiver's private key, 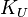 , associated to the receiver's identity,
, associated to the receiver's identity,  . The PKG must securely deliver the identity-specific private key to the receiver, and PKG-specific public parameter,
. The PKG must securely deliver the identity-specific private key to the receiver, and PKG-specific public parameter, 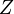 , to all parties. These distribution processes are not considered as part of the definition of this cryptographic scheme.
, to all parties. These distribution processes are not considered as part of the definition of this cryptographic scheme.
Preliminaries
The scheme uses two multiplicative groups 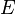 and
and 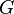 . It is assumed:
. It is assumed:
- The Diffie-Hellman problem is hard in
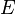 . Meaning that given two members of the group
. Meaning that given two members of the group  and
and  , it is hard to find
, it is hard to find  such that
such that ![\textstyle [x].P = Q](../I/m/34c418e380c65b3c3def8ed97ba18377.png) .
. - The Diffie-Hellman problem is hard in
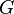 . Meaning that given two members of the group
. Meaning that given two members of the group  and
and  , it is hard to find
, it is hard to find  such that
such that 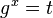 .
. - There is a bilinear map, a Tate-Lichtenbaum pairing,
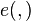 from E to G. This means that for
from E to G. This means that for  a member of
a member of 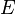 and for
and for 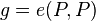 a member of
a member of  :
:
Frequently,  is a supersingular elliptic curve, such as
is a supersingular elliptic curve, such as 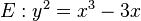 (over a finite field of prime order
(over a finite field of prime order 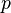 ). A generator
). A generator  of prime order
of prime order 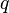 is chosen in
is chosen in 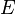 . The group
. The group 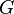 is the image due to the pairing of the group generated by
is the image due to the pairing of the group generated by  (in the extension field of degree 2 of the finite field of order p).
(in the extension field of degree 2 of the finite field of order p).
Two hash functions are also required, 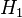 and
and 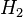 .
. 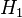 outputs a positive integer,
outputs a positive integer,  , such that
, such that  .
. 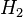 outputs
outputs  bits, where
bits, where  is the length of the message
is the length of the message 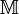 .
.
Key Generation
The PKG has a master secret 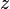 where
where 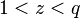 , and a public key
, and a public key ![\textstyle Z=[z].P](../I/m/cf9ab4816a18aa3779602d3884be4bf6.png) which is a point on
which is a point on 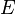 . The PKG generates the private key,
. The PKG generates the private key, 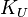 , for the user with identity
, for the user with identity 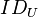 as follows:
as follows:
Encryption
To encrypt a non-repeating message 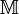 , the sender requires receiver's identity,
, the sender requires receiver's identity, 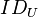 and the public PGK value
and the public PGK value 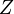 . The sender performs the following operation.
. The sender performs the following operation.
- Create:
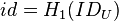
- The sender generates
 using
using 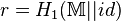
- Generate the point
 in
in 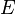 :
:
- Create the masked message:
- The encrypted output is:
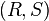
Note that messages may not repeat, as a repeated message to the same identity results in a repeated ciphertext. There is an extension to the protocol should messages potentially repeat.
Decryption
To decrypt a message encrypted to 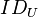 , the receiver requires the private key,
, the receiver requires the private key, 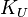 from the PKG and the public value
from the PKG and the public value 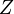 . The decryption procedure is as follows:
. The decryption procedure is as follows:
- Compute
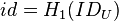
- Receive the encrypted message:
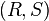 .
. - Compute:
- Extract the message:
- To verify the message, compute
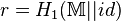 , and only accept the message if:
, and only accept the message if:
Demonstration of Algorithmic Correctness
The following equations demonstrate the correctness of the algorithm:
By the bilinear property of the map:
As a result:
Standardisation
There are two standards relating to this protocol:
- Initial standardisation of scheme was begun by IEEE in 2006.[4]
- The scheme was standardised by the IETF in 2012 within RFC 6508. The scheme is used as part of the MIKEY-SAKKE protocol, defined in RFC 6509.
Cryptographic Libraries and Implementations
The scheme is part of the MIRACL cryptographic library.
See also
References
- ↑ Sakai, Ryuichi; Kasahara, Masao (2003). "ID Based cryptosystems with pairing on elliptic curve" (PDF). Cryptography ePrint Archive. 2003/054.
- ↑ Chen, L.; Cheng, Z. "Security proof of Sakai-Kasahara's identity-based encryption scheme" (PDF). Cryptography ePrint Archive. 2005/226.
- ↑ Groves, L. (February 2012). Sakai-Kasahara Key Encryption (SAKKE). IETF. RFC 6508. https://tools.ietf.org/html/rfc6508.
- ↑ Barbosa, M. (June 2006). "SK-KEM: An Identity-Based KEM" (PDF). IEEE. P1363.3.
![\textstyle e(P,[x].P) = e([x].P,P) = e(P,P)^x = g^x](../I/m/a8dbd3400a19af75b051c7f168458c28.png)
![\textstyle K_U = [\frac{1}{z + H_1(ID_U)}].P](../I/m/50aece7c998dc14f7115e35b09df58cf.png)
![\textstyle R = [r].([id].P + Z)](../I/m/7f053a6f41e7a092341060f59da4d79d.png)
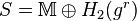
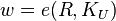
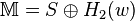
![\textstyle [r].([id].P + Z) \equiv R](../I/m/4c39a17da55a37c3f3eb1510c8354543.png)
![\textstyle w = e(R,K_U) = e([r].([id].P + Z),K_U) = e([r].([id].P + [z].P),K_U) = e([r(id+z)].P,K_U)](../I/m/1f1fa6abb4a5e44d95773acaec6bc21a.png)
![\textstyle w = e([r(id+z)].P,K_U)= e([r(id+z)].P,[\frac{1}{(id+z)}].P) = e(P,P)^{\frac{r(id+z)}{(id+z)}} = g^r](../I/m/d291fc3cf51ad3ba78d39eb2929d4531.png)